Ejemplo: gráficos cuantil-cuantil
Utilice la función qqplot para crear gráficos cuantil-cuantil (Q-Q).
Dos conjuntos de datos
Compare los cuantiles de dos conjuntos de datos en un gráfico Q-Q para comprobar si tienen la misma distribución.
1. Defina un conjunto de datos.

En la columna 2 se muestra el lote donde se realizó la medida y en la columna 3, la resistencia medida de las barras de nitrato de silicio aglomerado.
2. Extraiga las dos columnas de interés, 2 y 3.
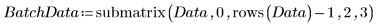
3. Llame a vlookup para dividir los datos en función de si las medidas se tomaron en el lote 1 o 2.
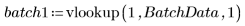
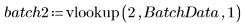
4. Calcule el primer y el tercer cuartil de cada lote.
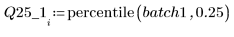
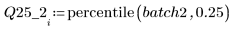
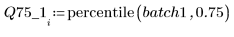
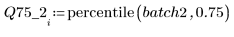
5. Trace un gráfico Q-Q y los cuantiles.
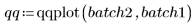
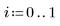
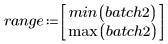
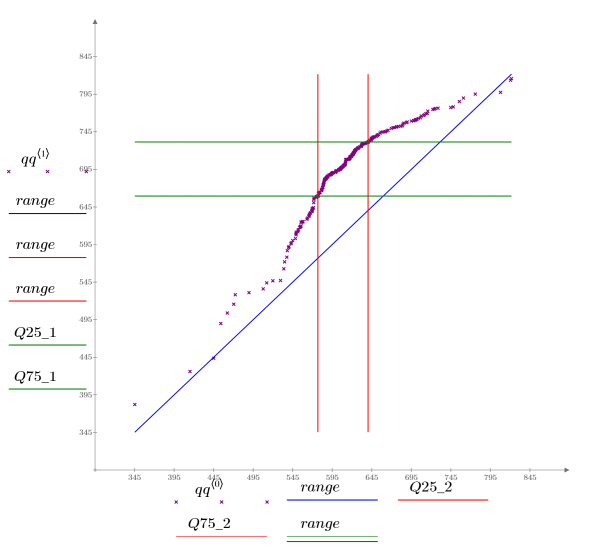
Se traza una línea de referencia de 1 a 1 para enfatizar la variación de los datos.
En el gráfico Q-Q se muestra que los dos lotes no comparten la misma distribución, aunque los valores para los percentiles muy pequeños y muy grandes sean similares. Los cuantiles del lote 1 son considerablemente superiores a los del lote 2, lo que sugiere condiciones de procesamiento muy diferentes.
Distribución normal
Determine si las medidas de un metro de flujo de calor se han tomado aleatoriamente. Verifique si las medidas se distribuyen normalmente comparándolas con la distribución normal en un gráfico Q-Q.
1. Defina un conjunto de datos que describa el flujo de calor.

2. Busque los puntos de datos del gráfico Q-Q normal.
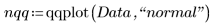
3. Busque la línea de trayectoria de ajuste para ver la proximidad de los cuantiles de datos a los cuantiles de distribución normal.
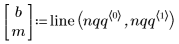
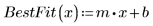
4. Trace el gráfico Q-Q y la línea de trayectoria de ajuste.
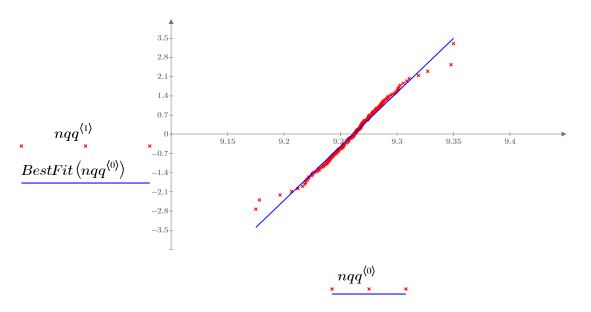
Una correlación muy estrecha con la línea de referencia indica que las muestras están distribuidas normalmente.
La comprobación de normalidad es una de las pruebas que se realizan para detectar valores atípicos.
Distribución de Weibull
Compruebe si un conjunto de datos sigue una distribución de Weibull.
1. Registre, en el vector R, el voltaje de error de aislamiento eléctrico para los cables sujetos a una tensión de voltaje creciente.
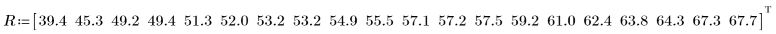
2. Trace un histograma con los datos.
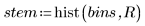
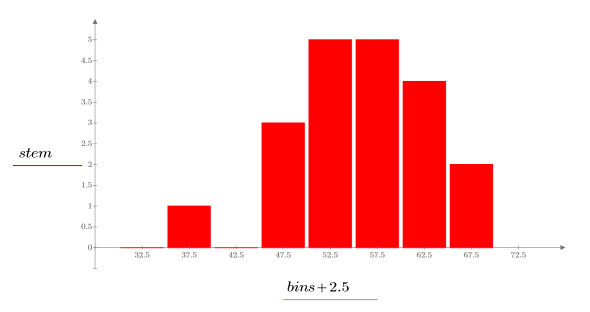
El histograma muestra que los datos no tienen una distribución normal. Los datos se inclinan hacia un lado. Los datos se pueden comparar con una distribución de Weibull en un gráfico Q-Q.
3. Busque los puntos de datos del gráfico Q-Q de Weibull.
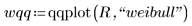
4. Busque la línea de trayectoria de ajuste para ver la proximidad de los cuantiles de datos a los cuantiles de distribución de Weibull.
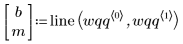
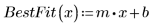
5. Trace el gráfico Q-Q y la línea de trayectoria de ajuste.
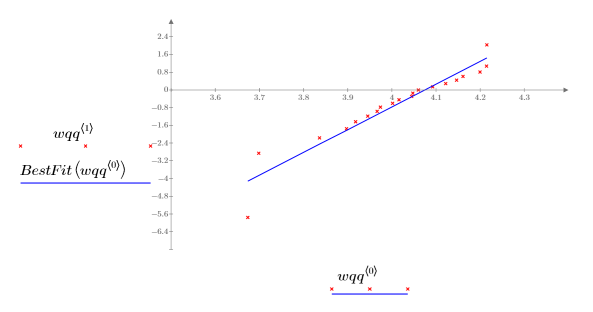
Una correlación estrecha con la línea de referencia indica que el conjunto de datos se puede modelar con una distribución de Weibull.
Para los gráficos Q-Q de Weibull se utiliza una escala logarítmica. |
Referencia
Lawless, J.F., Statistical Methods for Lifetime Data, segunda edición, Wiley-Interscience, 2002.