Ejemplo: distribución de probabilidad acumulada y densidad de probabilidad
Utilice las funciones dnorm, pnorm, cnorm y qnorm para demostrar las diferencias entre varias funciones de probabilidad.
1. Defina la media y la desviación estándar de una distribución normal.
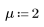
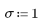
2. Trace la densidad de probabilidad (azul) y la probabilidad acumulada (negro y rojo) de las distribuciones normales.
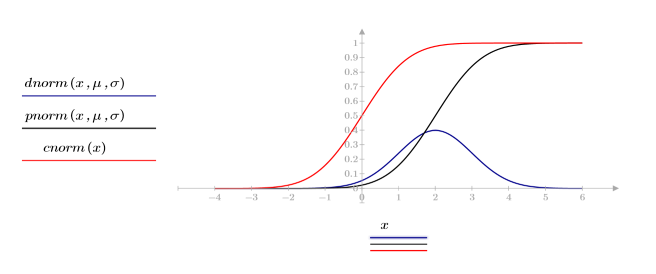
La función dnorm calcula la densidad de probabilidad en x de una distribución normal con media μ y desviación estándar σ. La función pnorm calcula la distribución de probabilidad acumulada de la distribución normal. La función cnorm es la distribución de probabilidad acumulada de la distribución normal con μ = 0 y σ = 1.
3. Utilice la función qnorm para calcular el valor de x si el área por debajo de la curva, de - ∞ a x, es la mitad del área debajo de toda la curva.
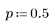
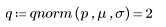
En este caso, el valor de x es igual a la media, como se puede confirmar con la siguiente fórmula:
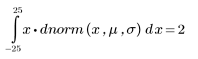
La densidad de probabilidad en q se recupera fácilmente mediante la función pnorm, que es la inversa de la función qnorm:
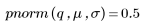
4. Utilice la función qnorm para buscar los percentiles 75, 90 y 95 de la distribución normal.
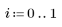
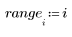
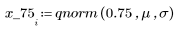
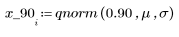
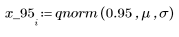
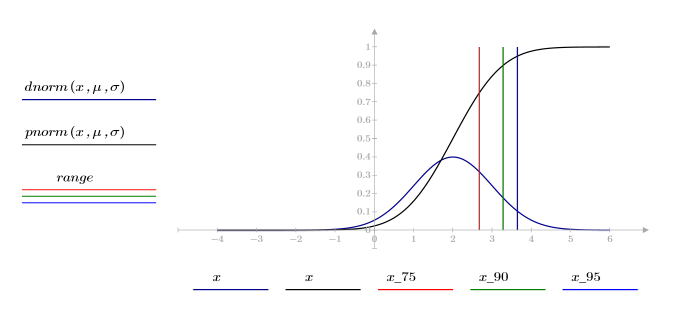
5. Trace la densidad de probabilidad (azul) y la probabilidad acumulada (negro) de una distribución normal sumando los percentiles calculados anteriormente (75 %: rojo, 90 %: verde, 95 %: azul).