Ejemplo: análisis de componentes principales 2
Utilice las funciones Nipals y Nipals2 para analizar datos complejos, como el espectro NIR (infrarrojo cercano) de unas pastillas con cinco dosis diferentes de ingredientes activos (los datos son cortesía de Bruker Optics, Inc.). Se puede crear un modelo para distinguir cada dosis según el espectro, aunque se desconozcan las dosis reales. Este modelo se puede utilizar para el control de calidad cuando se fabriquen más pastillas.
1. Defina el siguiente conjunto de datos:
|
|
Este conjunto de datos describe un estudio doble ciego en una prueba clínica.
|

La primera columna es el número de onda (1/longitud de onda) en cm-1. Existen cinco espectros secuenciales de cada dosis, que conforman las otras 25 columnas.
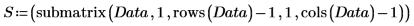
3. Utilice las funciones max y match para buscar el valor máximo y el espectro que lo contiene. Puesto que los valores de datos son muy pequeños, defina TOL en un valor aún más pequeño.
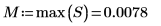
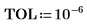
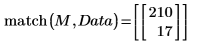
El valor máximo está en la fila 210 y la columna 17 de la matriz de datos.
4. Trace los dos primeros espectros de cada dosis; el total es de 10 conjuntos de datos. Los pares de conjuntos de datos son las columnas [1,2], [6,7], [11,12], [16,17] y [21,22] de la matriz Data.
◦ Para obtener una escala razonable para el eje horizontal, divida los números de onda por 1000. De forma similar, puesto que los valores de los espectros son pequeños, multiplíquelos por 1000.
◦ Utilice un marcador horizontal para mostrar el valor máximo de los espectros.
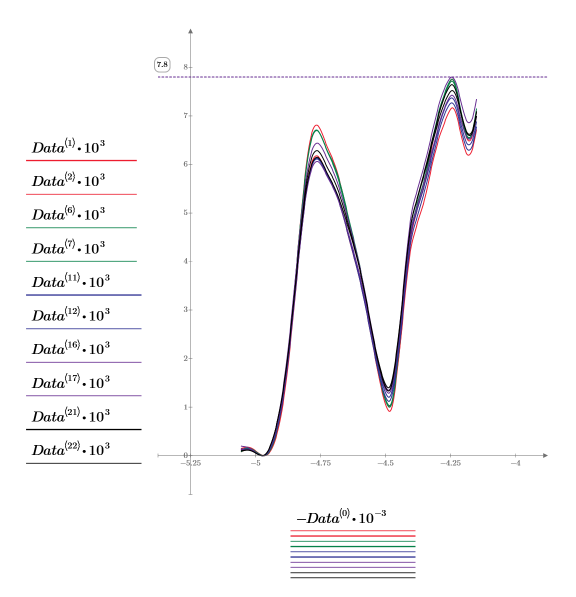
◦ Los números de onda se trazan, por convención, en orden descendente. Por lo tanto, se niega Data<0> para mostrar los números de onda en el orden correcto.
◦ No puede utilizarse ninguna parte del espectro para distinguir fácilmente una dosis de otra: todas tienen la misma forma básica y valores de absorbancia similares.
◦ La mayoría de los datos son redundantes. Cada espectro tiene 236 puntos y, por lo tanto, 236 variables medidas (absorción para una longitud de onda luminosa determinada), pero la variación de estos puntos está claramente interrelacionada.
5. Divida la matriz de Data en dos conjuntos de datos: los números de onda (columna 0) y los espectros de cada pastilla (submatriz S). Para cumplir la convención común, transponga los espectros de cada pastilla de modo que cada columna corresponda a una variable independiente.
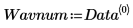
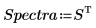
6. Defina el número de componentes principales, así como el número máximo de iteraciones antes de aplicar la función Nipals a los datos. La función Nipals centra los datos y resta el espectro medio de cada fila.
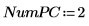
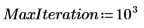
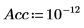
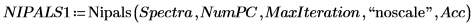
7. Elija un espectro para recrearlo.
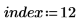
8. Extraiga las puntuaciones y las cargas de la salida de la función Nipals.
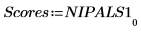
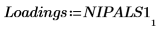
9. Utilice la función mean para calcular el espectro medio.
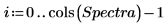
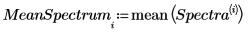
10. Para realizar un cálculo aproximado del espectro original, multiplique la matriz de los vectores de carga por la matriz de puntuaciones y, a continuación, añada el espectro medio.
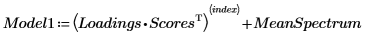
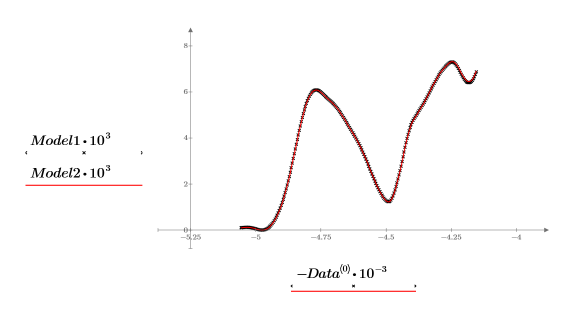
11. Trace los espectros original y reconstruido. Aplique una escala a los ejes horizontal y vertical para obtener valores razonables.
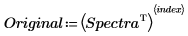
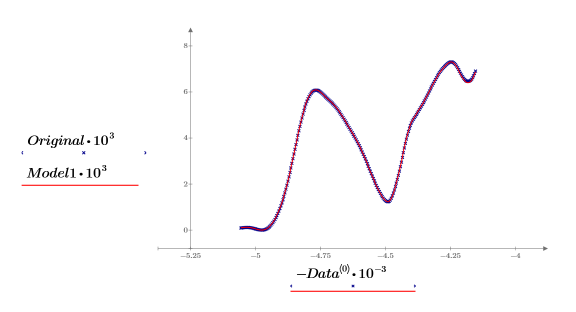
Todos los espectros se representan correctamente utilizando únicamente dos componentes principales para el análisis de componentes principales.
12. Reorganice las puntuaciones en dos matrices. Cada columna de las matrices representa las puntuaciones de una de las cinco dosis de pastillas.
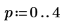
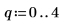
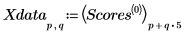
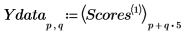
13. Trace las puntuaciones del primer factor con respecto a las puntuaciones del segundo factor. Cada dosis se muestra con un color diferente.
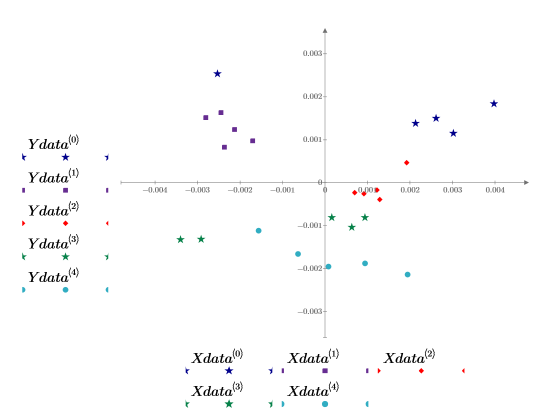
La agrupación de algunos de los datos es evidente, pero aún resulta difícil distinguir las dosis entre sí. Podría resultar útil añadir una tercera puntuación al gráfico.
14. Utilice la función Nipals2 para añadir cuatro componentes principales al modelo creado con dos componentes principales.
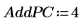
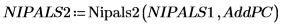
La matriz de salida de NIPALS2 presenta la misma forma que la de NIPALS, pero tiene columnas y filas adicionales correspondientes a los componentes principales adicionales. El número de puntuaciones y cargas ha aumentado ahora hasta llegar a seis.
15. Extraiga las cargas y las puntuaciones de la matriz NIPALS2 para crear un modelo nuevo del espectro elegido.
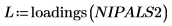
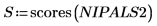
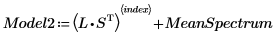
16. Trace y compare los dos modelos del espectro elegido. Aplique una escala al eje horizontal y vertical para obtener valores razonables.
17. Extraiga la varianza acumulada de NIPALS2.
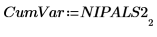
18. Trace la varianza acumulada con respecto al número de componentes principales.
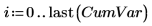
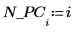
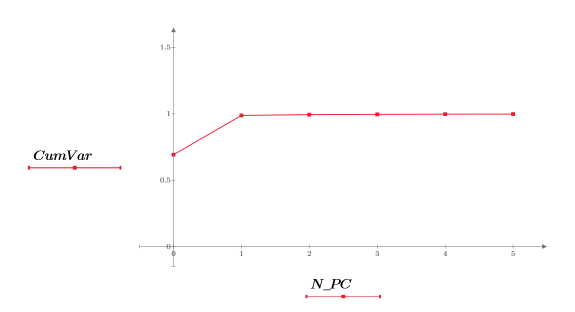
Los dos primeros componentes principales (PC) representan el 99 % de la varianza, pero el tercer PC resulta esencial para agrupar los datos por dosis. El análisis de componentes principales limita los datos a los factores más dominantes, pero no a los más pertinentes.