Ejemplo: Regresión no lineal 2
Utilice la función LeastSquaresFit para realizar una regresión no lineal. El solver LeastSquaresFit es el que proporciona más flexibilidad para resolver problemas de regresión no lineal. Permite introducir ecuaciones de restricción para cualquiera de los parámetros dependientes, límites inferior y superior para los parámetros, desviaciones estándar de los valores x y un límite de confianza para el cálculo.
LeastSquaresFit
1. Defina un conjunto de datos.
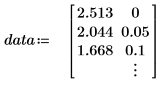
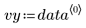
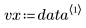
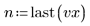
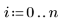
Estos datos se toman de un ejemplo tratado en el sitio Web del NIST. Los datos se generaron con una precisión de 14 dígitos utilizando la siguiente ecuación:
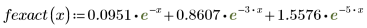
2. Defina una función de ajuste.
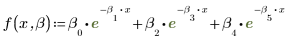
Los parámetros individuales anteriores son elementos de un vector β. También puede especificar la función de entrada con nombres de variable individuales, en vez de elementos de un vector:
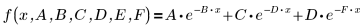
3. Indique valores de prueba.
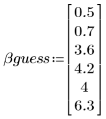
4. Defina el límite de confianza de los parámetros.
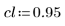
5. Llame a la función LeastSquaresFit.
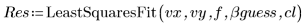
El solver utiliza programación cuadrática (QP) secuencial para resolver el problema de mínimos cuadrados resultante. Al introducir variables adicionales, el problema original se convierte en un problema de programación no lineal restringido de igualdad general, que suele ser más rápido y estable que otros métodos.
6. Observe el vector de salida que devuelve la función LeastSquaresFit.
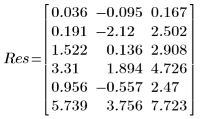
◦ La primera columna de salida contiene los valores de los parámetros ajustados. La segunda columna contiene el contorno izquierdo y la tercera columna, el contorno derecho del intervalo de confianza de los parámetros.
◦ Los límites de confianza del 95 % de los parámetros cubren un rango bastante amplio, lo que demuestra que el ajuste es difícil y los parámetros individuales pueden variar considerablemente. Como consecuencia, los valores de los parámetros ajustados difieren de los valores correctos registrados en el sitio Web del NIST:
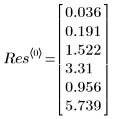

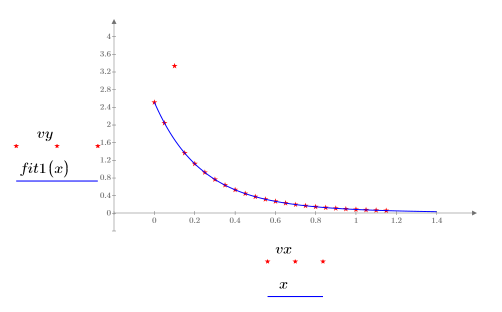
7. Trace los datos, el ajuste de mínimos cuadrados y el ajuste del NIST.
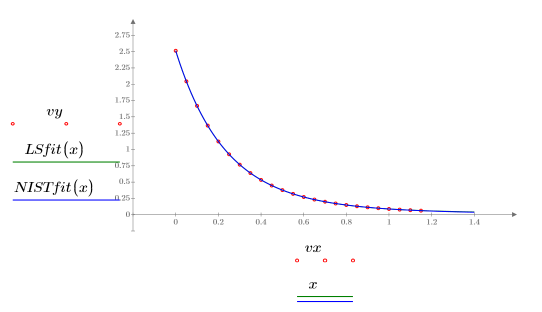
8. Compare el ajuste de mínimos cuadrados con los datos originales:
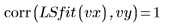
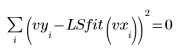
El ajuste se acerca a la convergencia, pero podría beneficiarse de un ajuste en la tolerancia de convergencia. Esto se puede realizar mediante uno de los argumentos opcionales de la función LeastSquaresFit.
Restricciones, desviación estándar y tolerancia
Existen varios argumentos opcionales para LeastSquaresFit:
• Vector de desviación estándar
• Matriz de límites inferior y superior
• Precisión
Puede utilizar cualquiera de los argumentos opcionales por sí solo; sin embargo, si se introducen varios argumentos, su orden es importante.
1. Modifique uno de los valores de datos para simular una medición errónea.
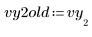
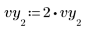
2. Especifique límites inferior y superior para restringir los valores de ajuste.
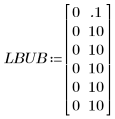
Los límites se encuentran definidos fuera de los valores esperados de los parámetros, ya que en este caso no hay ningún límite conocido.
3. Defina un vector de desviaciones estándar para cada valor y que enmascare el valor atípico.
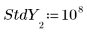
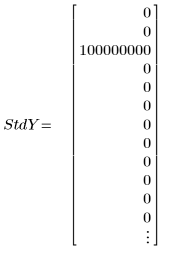
◦ El valor grande de 108 en la desviación estándar quita de forma eficaz la medición errónea del cálculo.
◦ Cuando se introduce un vector de desviación estándar como un argumento en la función LeastSquaresFit, el solver minimiza la función siguiente:
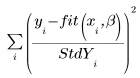
Si la desviación estándar es 0 para un punto, se utiliza la función original no desviada para dicho punto, es decir, StdYi se define en 1.
4. Defina la precisión para aplicar una tolerancia de convergencia más estricta al cálculo (por defecto, es 10-7).
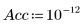
5. Llame a la función LeastSquaresFit con y sin la desviación estándar.
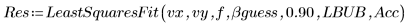
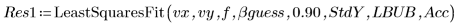
◦ El cálculo sin máscara falla porque los límites de confianza son demasiado grandes.
◦ Los nuevos parámetros se acercan más a los valores del NIST:
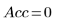
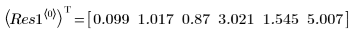
6. Trace los datos con el valor atípico y el ajuste enmascarado.
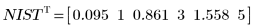
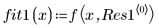
Referencia
Los datos de este ejemplo se han extraído de Lanczos, C., Applied Analysis, Prentice Hall, 1956, páginas 272-280, tal como se indica en Statistical Reference Dataset Archive, el archivo de datos de referencia estadística del NIST.