Ejemplo: funciones modificadas de Bessel de primera especie

Funciones > Funciones especiales > Funciones de Bessel > Ejemplo: funciones modificadas de Bessel de primera especie

Muestre la relación entre las funciones I0, I1 e In. Muestre también las relaciones entre estas funciones y sus versiones escaladas.

1. Defina dos variables de rango de paso:

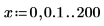
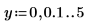
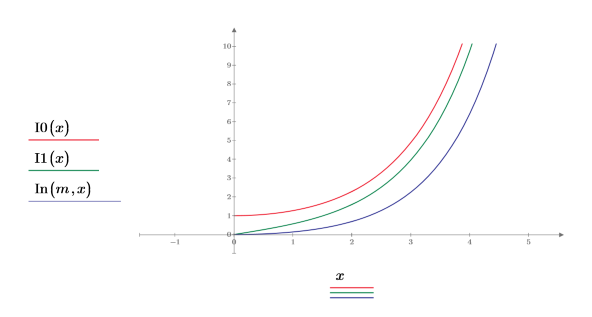
2. Trace las funciones I0 y I1. Añada la función de segundo orden In al gráfico:

<region id="ID0ET556" actualWidth="591.66857242139008" actualHeight="316.8" top="115.20000000000002" left="0" height="316.8" width="591.66857242139008" xmlns="http://schemas.mathsoft.com/worksheet50">
  <plot background-type="white" origin-positioning="true">
    <xyPlot>
      <title class="- topic/title " wwtype:type="Paragraph" xmlns:wwtype="urn:WebWorks-Type-Schema" />
      <legend />
      <traces>
        <trace resultRef="48">
          <traceStyle color="#FFED1D2F" symbol="none" line-weight="1" line-style="Solid">lines</traceStyle>
        </trace>
        <trace resultRef="49">
          <traceStyle color="#FF068149" symbol="none" line-weight="1" line-style="Solid">lines</traceStyle>
        </trace>
        <trace resultRef="50">
          <traceStyle color="#FF2E3192" symbol="none" line-weight="1" line-style="Solid">lines</traceStyle>
        </trace>
      </traces>
      <graph-size width="438.06857242139" height="240" />
      <axes>
        <xAxis rank="1" legend-position="PlotBoundaryBottom" start="-1" end="5">
          <axisLine position="origin" positionticmark="0" legendWidth="60.93" />
          <axisGrid>
            <gridFrequency>7</gridFrequency>
            <gridLabels display="true" />
            <gridLines />
            <tickMarks display="true" />
          </axisGrid>
          <axisLabel />
          <markers />
          <plotEquations>
            <plotEquation>
              <math>
                <id labels="VARIABLE" xml:space="preserve" label-is-contextual="true" xmlns="http://schemas.mathsoft.com/math50">x</id>
              </math>
              <math>
                <placeholder xmlns="http://schemas.mathsoft.com/math50" />
              </math>
            </plotEquation>
          </plotEquations>
          <xyDomain scale-type="linear" auto-scale="true">
            <startValue resultRef="51">
              <real xmlns="http://schemas.mathsoft.com/math50">-1</real>
            </startValue>
            <secondTickValue resultRef="52">
              <real xmlns="http://schemas.mathsoft.com/math50">0</real>
            </secondTickValue>
            <endValue resultRef="53">
              <real xmlns="http://schemas.mathsoft.com/math50">5</real>
            </endValue>
          </xyDomain>
        </xAxis>
        <yAxis rank="1" legend-position="PlotBoundaryLeft" start="0" end="10">
          <axisLine position="origin" positionticmark="1" legendWidth="111.28" />
          <axisGrid>
            <gridFrequency>11</gridFrequency>
            <gridLabels display="true" />
            <gridLines />
            <tickMarks display="true" />
          </axisGrid>
          <axisLabel />
          <markers />
          <plotEquations>
            <plotEquation>
              <math>
                <apply xmlns="http://schemas.mathsoft.com/math50">
                  <id labels="FUNCTION" xml:space="preserve">I0</id>
                  <id labels="VARIABLE" xml:space="preserve" label-is-contextual="true">x</id>
                </apply>
              </math>
              <math>
                <placeholder xmlns="http://schemas.mathsoft.com/math50" />
              </math>
            </plotEquation>
            <plotEquation>
              <math>
                <apply xmlns="http://schemas.mathsoft.com/math50">
                  <id labels="FUNCTION" xml:space="preserve">I1</id>
                  <id labels="VARIABLE" xml:space="preserve" label-is-contextual="true">x</id>
                </apply>
              </math>
              <math>
                <placeholder xmlns="http://schemas.mathsoft.com/math50" />
              </math>
            </plotEquation>
            <plotEquation>
              <math>
                <apply xmlns="http://schemas.mathsoft.com/math50">
                  <id labels="FUNCTION" xml:space="preserve">In</id>
                  <sequence>
                    <id labels="VARIABLE" xml:space="preserve" label-is-contextual="true">m</id>
                    <id labels="VARIABLE" xml:space="preserve" label-is-contextual="true">x</id>
                  </sequence>
                </apply>
              </math>
              <math>
                <placeholder xmlns="http://schemas.mathsoft.com/math50" />
              </math>
            </plotEquation>
          </plotEquations>
          <xyDomain scale-type="linear" auto-scale="true">
            <startValue resultRef="54">
              <real xmlns="http://schemas.mathsoft.com/math50">0</real>
            </startValue>
            <secondTickValue resultRef="55">
              <real xmlns="http://schemas.mathsoft.com/math50">1</real>
            </secondTickValue>
            <endValue resultRef="56">
              <real xmlns="http://schemas.mathsoft.com/math50">10</real>
            </endValue>
          </xyDomain>
        </yAxis>
      </axes>
    </xyPlot>
  </plot>
</region>

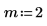
3. Trace la función de quinto y octavo orden In:

<region id="ID0EHA66" actualWidth="590.86857242139" actualHeight="316.8" top="441.60000000000008" left="0" height="316.8" width="590.86857242139" xmlns="http://schemas.mathsoft.com/worksheet50">
  <plot background-type="white" origin-positioning="true">
    <xyPlot>
      <title class="- topic/title " wwtype:type="Paragraph" xmlns:wwtype="urn:WebWorks-Type-Schema" />
      <legend />
      <traces>
        <trace resultRef="57">
          <traceStyle color="#FFED1D2F" symbol="none" line-weight="1" line-style="Solid">lines</traceStyle>
        </trace>
        <trace resultRef="58">
          <traceStyle color="#FF068149" symbol="none" line-weight="1" line-style="Solid">lines</traceStyle>
        </trace>
        <trace resultRef="59">
          <traceStyle color="#FF2E3192" symbol="none" line-weight="1" line-style="Solid">lines</traceStyle>
        </trace>
        <trace resultRef="60">
          <traceStyle color="#FF2E3192" symbol="none" line-weight="1" line-style="Dash">lines</traceStyle>
        </trace>
        <trace resultRef="61">
          <traceStyle color="#FFCA5053" symbol="none" line-weight="1" line-style="Dash">lines</traceStyle>
        </trace>
      </traces>
      <graph-size width="418.06857242139" height="240" />
      <axes>
        <xAxis rank="1" legend-position="PlotBoundaryBottom" start="-1" end="7">
          <axisLine position="origin" positionticmark="0" legendWidth="60.93" />
          <axisGrid>
            <gridFrequency>9</gridFrequency>
            <gridLabels display="true" />
            <gridLines />
            <tickMarks display="true" />
          </axisGrid>
          <axisLabel />
          <markers />
          <plotEquations>
            <plotEquation>
              <math>
                <id labels="VARIABLE" xml:space="preserve" label-is-contextual="true" xmlns="http://schemas.mathsoft.com/math50">x</id>
              </math>
              <math>
                <placeholder xmlns="http://schemas.mathsoft.com/math50" />
              </math>
            </plotEquation>
          </plotEquations>
          <xyDomain scale-type="linear" auto-scale="true">
            <startValue resultRef="62">
              <real xmlns="http://schemas.mathsoft.com/math50">-1</real>
            </startValue>
            <secondTickValue resultRef="63">
              <real xmlns="http://schemas.mathsoft.com/math50">0</real>
            </secondTickValue>
            <endValue resultRef="64">
              <real xmlns="http://schemas.mathsoft.com/math50">7</real>
            </endValue>
          </xyDomain>
        </xAxis>
        <yAxis rank="1" legend-position="PlotBoundaryLeft" start="0" end="2">
          <axisLine position="origin" positionticmark="1" legendWidth="134.01" />
          <axisGrid>
            <gridFrequency>3</gridFrequency>
            <gridLabels display="true" />
            <gridLines />
            <tickMarks display="true" />
          </axisGrid>
          <axisLabel />
          <markers />
          <plotEquations>
            <plotEquation>
              <math>
                <apply xmlns="http://schemas.mathsoft.com/math50">
                  <id labels="FUNCTION" xml:space="preserve">I0</id>
                  <id labels="VARIABLE" xml:space="preserve" label-is-contextual="true">x</id>
                </apply>
              </math>
              <math>
                <placeholder xmlns="http://schemas.mathsoft.com/math50" />
              </math>
            </plotEquation>
            <plotEquation>
              <math>
                <apply xmlns="http://schemas.mathsoft.com/math50">
                  <id labels="FUNCTION" xml:space="preserve">I1</id>
                  <id labels="VARIABLE" xml:space="preserve" label-is-contextual="true">x</id>
                </apply>
              </math>
              <math>
                <placeholder xmlns="http://schemas.mathsoft.com/math50" />
              </math>
            </plotEquation>
            <plotEquation>
              <math>
                <apply xmlns="http://schemas.mathsoft.com/math50">
                  <id labels="FUNCTION" xml:space="preserve">In</id>
                  <sequence>
                    <id labels="VARIABLE" xml:space="preserve" label-is-contextual="true">m</id>
                    <id labels="VARIABLE" xml:space="preserve" label-is-contextual="true">x</id>
                  </sequence>
                </apply>
              </math>
              <math>
                <placeholder xmlns="http://schemas.mathsoft.com/math50" />
              </math>
            </plotEquation>
            <plotEquation>
              <math>
                <apply xmlns="http://schemas.mathsoft.com/math50">
                  <id labels="FUNCTION" xml:space="preserve">In</id>
                  <sequence>
                    <apply>
                      <plus />
                      <id labels="VARIABLE" xml:space="preserve" label-is-contextual="true">m</id>
                      <real>3</real>
                    </apply>
                    <id labels="VARIABLE" xml:space="preserve" label-is-contextual="true">x</id>
                  </sequence>
                </apply>
              </math>
              <math>
                <placeholder xmlns="http://schemas.mathsoft.com/math50" />
              </math>
            </plotEquation>
            <plotEquation>
              <math>
                <apply xmlns="http://schemas.mathsoft.com/math50">
                  <id labels="FUNCTION" xml:space="preserve">In</id>
                  <sequence>
                    <apply>
                      <plus />
                      <id labels="VARIABLE" xml:space="preserve" label-is-contextual="true">m</id>
                      <real>6</real>
                    </apply>
                    <id labels="VARIABLE" xml:space="preserve" label-is-contextual="true">x</id>
                  </sequence>
                </apply>
              </math>
              <math>
                <placeholder xmlns="http://schemas.mathsoft.com/math50" />
              </math>
            </plotEquation>
          </plotEquations>
          <xyDomain scale-type="linear" auto-scale="true">
            <startValue resultRef="65">
              <real xmlns="http://schemas.mathsoft.com/math50">0</real>
            </startValue>
            <secondTickValue resultRef="66">
              <real xmlns="http://schemas.mathsoft.com/math50">1</real>
            </secondTickValue>
            <endValue resultRef="67">
              <real xmlns="http://schemas.mathsoft.com/math50">2</real>
            </endValue>
          </xyDomain>
        </yAxis>
      </axes>
    </xyPlot>
  </plot>
</region>

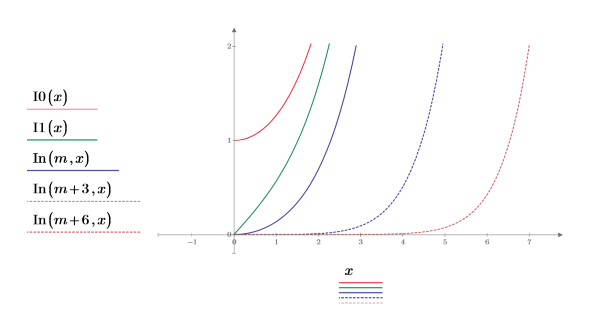
• Cuanto más alto sea el orden de la función In, más brusca será la transición desde cero.

• Solo la función I0 tiene su origen en (x=0,y=1). El resto de órdenes tienen su origen en (x=0,y=0)..

4. Cree un gráfico para mostrar que I0(y)=In(0,y). Redefina los valores de marca de graduación para ampliar el eje X con el fin de mostrar más detalles:

<region id="ID0EJF66" actualWidth="572.46857242139" actualHeight="297.6" top="883.20000000000016" left="0" height="297.6" width="572.46857242139" xmlns="http://schemas.mathsoft.com/worksheet50">
  <plot background-type="white" origin-positioning="true">
    <xyPlot>
      <title class="- topic/title " wwtype:type="Paragraph" xmlns:wwtype="urn:WebWorks-Type-Schema" />
      <legend />
      <traces>
        <trace resultRef="68">
          <traceStyle color="#FFED1D2F" symbol="none" line-weight="1" line-style="Solid">lines</traceStyle>
        </trace>
        <trace resultRef="69">
          <traceStyle color="#FF068149" symbol="circle" line-weight="1" line-style="None">lines</traceStyle>
        </trace>
      </traces>
      <graph-size width="438.06857242139" height="240" />
      <axes>
        <xAxis rank="1" legend-position="PlotBoundaryBottom" start="0" end="5">
          <axisLine position="origin" positionticmark="0" legendWidth="60.74" />
          <axisGrid>
            <gridFrequency>6</gridFrequency>
            <gridLabels display="true" />
            <gridLines />
            <tickMarks display="true" />
          </axisGrid>
          <axisLabel />
          <markers />
          <plotEquations>
            <plotEquation>
              <math>
                <id labels="VARIABLE" xml:space="preserve" label-is-contextual="true" xmlns="http://schemas.mathsoft.com/math50">y</id>
              </math>
              <math>
                <placeholder xmlns="http://schemas.mathsoft.com/math50" />
              </math>
            </plotEquation>
          </plotEquations>
          <xyDomain scale-type="linear" auto-scale="true">
            <startValue>
              <placeholder xmlns="http://schemas.mathsoft.com/math50" />
            </startValue>
            <secondTickValue resultRef="70">
              <real xmlns="http://schemas.mathsoft.com/math50">1</real>
            </secondTickValue>
            <endValue>
              <placeholder xmlns="http://schemas.mathsoft.com/math50" />
            </endValue>
          </xyDomain>
        </xAxis>
        <yAxis rank="1" legend-position="PlotBoundaryLeft" start="0" end="2">
          <axisLine position="origin" positionticmark="0" legendWidth="105.416666666667" />
          <axisGrid>
            <gridFrequency>3</gridFrequency>
            <gridLabels display="true" />
            <gridLines />
            <tickMarks display="true" />
          </axisGrid>
          <axisLabel />
          <markers />
          <plotEquations>
            <plotEquation>
              <math>
                <apply xmlns="http://schemas.mathsoft.com/math50">
                  <id labels="FUNCTION" xml:space="preserve" label-is-contextual="true">I0</id>
                  <id labels="VARIABLE" xml:space="preserve" label-is-contextual="true">y</id>
                </apply>
              </math>
              <math>
                <placeholder xmlns="http://schemas.mathsoft.com/math50" />
              </math>
            </plotEquation>
            <plotEquation>
              <math>
                <apply xmlns="http://schemas.mathsoft.com/math50">
                  <id labels="FUNCTION" xml:space="preserve" label-is-contextual="true">In</id>
                  <sequence>
                    <real>0</real>
                    <id labels="VARIABLE" xml:space="preserve" label-is-contextual="true">y</id>
                  </sequence>
                </apply>
              </math>
              <math>
                <placeholder xmlns="http://schemas.mathsoft.com/math50" />
              </math>
            </plotEquation>
          </plotEquations>
          <xyDomain scale-type="linear" auto-scale="true">
            <startValue resultRef="71">
              <real xmlns="http://schemas.mathsoft.com/math50">0</real>
            </startValue>
            <secondTickValue resultRef="72">
              <real xmlns="http://schemas.mathsoft.com/math50">1</real>
            </secondTickValue>
            <endValue resultRef="73">
              <real xmlns="http://schemas.mathsoft.com/math50">2</real>
            </endValue>
          </xyDomain>
        </yAxis>
      </axes>
    </xyPlot>
  </plot>
</region>

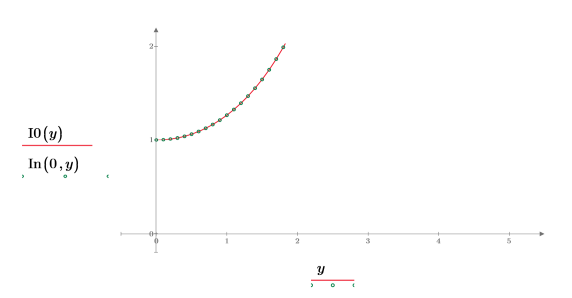
5. Cree un gráfico para mostrar que I1(y)=In(1,y). Redefina los valores de marca de graduación para ampliar el eje X con el fin de mostrar más detalles:

<region id="ID0E4G66" actualWidth="572.46857242139" actualHeight="297.6" top="1190.4" left="0" height="297.6" width="572.46857242139" xmlns="http://schemas.mathsoft.com/worksheet50">
  <plot background-type="white" origin-positioning="true">
    <xyPlot>
      <title class="- topic/title " wwtype:type="Paragraph" xmlns:wwtype="urn:WebWorks-Type-Schema" />
      <legend />
      <traces>
        <trace resultRef="74">
          <traceStyle color="#FFED1D2F" symbol="none" line-weight="1" line-style="Solid">lines</traceStyle>
        </trace>
        <trace resultRef="75">
          <traceStyle color="#FF2E3192" symbol="circle" line-weight="1" line-style="None">lines</traceStyle>
        </trace>
      </traces>
      <graph-size width="438.06857242139" height="240" />
      <axes>
        <xAxis rank="1" legend-position="PlotBoundaryBottom" start="0" end="5">
          <axisLine position="origin" positionticmark="0" legendWidth="60.74" />
          <axisGrid>
            <gridFrequency>6</gridFrequency>
            <gridLabels display="true" />
            <gridLines />
            <tickMarks display="true" />
          </axisGrid>
          <axisLabel />
          <markers />
          <plotEquations>
            <plotEquation>
              <math>
                <id labels="VARIABLE" xml:space="preserve" label-is-contextual="true" xmlns="http://schemas.mathsoft.com/math50">y</id>
              </math>
              <math>
                <placeholder xmlns="http://schemas.mathsoft.com/math50" />
              </math>
            </plotEquation>
          </plotEquations>
          <xyDomain scale-type="linear" auto-scale="true">
            <startValue>
              <placeholder xmlns="http://schemas.mathsoft.com/math50" />
            </startValue>
            <secondTickValue resultRef="76">
              <real xmlns="http://schemas.mathsoft.com/math50">1</real>
            </secondTickValue>
            <endValue>
              <placeholder xmlns="http://schemas.mathsoft.com/math50" />
            </endValue>
          </xyDomain>
        </xAxis>
        <yAxis rank="1" legend-position="PlotBoundaryLeft" start="0" end="2">
          <axisLine position="origin" positionticmark="0" legendWidth="105.416666666667" />
          <axisGrid>
            <gridFrequency>3</gridFrequency>
            <gridLabels display="true" />
            <gridLines />
            <tickMarks display="true" />
          </axisGrid>
          <axisLabel />
          <markers />
          <plotEquations>
            <plotEquation>
              <math>
                <apply xmlns="http://schemas.mathsoft.com/math50">
                  <id labels="FUNCTION" xml:space="preserve" label-is-contextual="true">I1</id>
                  <id labels="VARIABLE" xml:space="preserve" label-is-contextual="true">y</id>
                </apply>
              </math>
              <math>
                <placeholder xmlns="http://schemas.mathsoft.com/math50" />
              </math>
            </plotEquation>
            <plotEquation>
              <math>
                <apply xmlns="http://schemas.mathsoft.com/math50">
                  <id labels="FUNCTION" xml:space="preserve" label-is-contextual="true">In</id>
                  <sequence>
                    <real>1</real>
                    <id labels="VARIABLE" xml:space="preserve" label-is-contextual="true">y</id>
                  </sequence>
                </apply>
              </math>
              <math>
                <placeholder xmlns="http://schemas.mathsoft.com/math50" />
              </math>
            </plotEquation>
          </plotEquations>
          <xyDomain scale-type="linear" auto-scale="true">
            <startValue resultRef="77">
              <real xmlns="http://schemas.mathsoft.com/math50">0</real>
            </startValue>
            <secondTickValue resultRef="78">
              <real xmlns="http://schemas.mathsoft.com/math50">1</real>
            </secondTickValue>
            <endValue resultRef="79">
              <real xmlns="http://schemas.mathsoft.com/math50">2</real>
            </endValue>
          </xyDomain>
        </yAxis>
      </axes>
    </xyPlot>
  </plot>
</region>

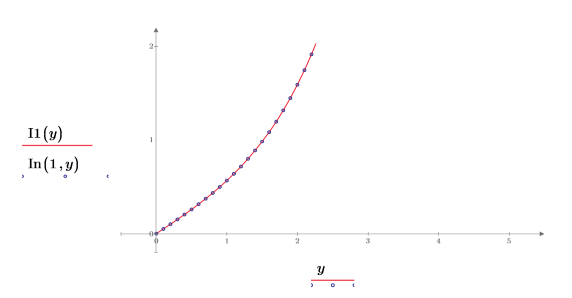
6. Utilice la evaluación simbólica para mostrar la relación entre cada función y su versión escalada:

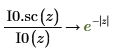
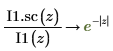
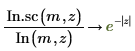
7. Utilice un gráfico para mostrar que:

<region id="ID0EHL66" actualWidth="533.86857242139024" actualHeight="297.6" top="1785.6000000000004" left="0" height="297.6" width="533.86857242139024" xmlns="http://schemas.mathsoft.com/worksheet50">
  <plot background-type="white" origin-positioning="true">
    <xyPlot>
      <title class="- topic/title " wwtype:type="Paragraph" xmlns:wwtype="urn:WebWorks-Type-Schema" />
      <legend />
      <traces>
        <trace resultRef="84">
          <traceStyle color="#FFED1D2F" symbol="none" line-weight="1" line-style="Solid">lines</traceStyle>
        </trace>
        <trace resultRef="85">
          <traceStyle color="#FF662D91" symbol="circle" line-weight="1" line-style="None">lines</traceStyle>
        </trace>
      </traces>
      <graph-size width="380.26857242139" height="240" />
      <axes>
        <xAxis rank="1" legend-position="PlotBoundaryBottom" start="0" end="5">
          <axisLine position="origin" positionticmark="0" legendWidth="60.74" />
          <axisGrid>
            <gridFrequency>6</gridFrequency>
            <gridLabels display="true" />
            <gridLines />
            <tickMarks display="true" />
          </axisGrid>
          <axisLabel />
          <markers />
          <plotEquations>
            <plotEquation>
              <math>
                <id labels="VARIABLE" xml:space="preserve" label-is-contextual="true" xmlns="http://schemas.mathsoft.com/math50">y</id>
              </math>
              <math>
                <placeholder xmlns="http://schemas.mathsoft.com/math50" />
              </math>
            </plotEquation>
          </plotEquations>
          <xyDomain scale-type="linear" auto-scale="true">
            <startValue>
              <placeholder xmlns="http://schemas.mathsoft.com/math50" />
            </startValue>
            <secondTickValue resultRef="86">
              <real xmlns="http://schemas.mathsoft.com/math50">1</real>
            </secondTickValue>
            <endValue>
              <placeholder xmlns="http://schemas.mathsoft.com/math50" />
            </endValue>
          </xyDomain>
        </xAxis>
        <yAxis rank="1" legend-position="PlotBoundaryLeft" start="0" end="2">
          <axisLine position="origin" positionticmark="0" legendWidth="123.773333333333" />
          <axisGrid>
            <gridFrequency>3</gridFrequency>
            <gridLabels display="true" />
            <gridLines />
            <tickMarks display="true" />
          </axisGrid>
          <axisLabel />
          <markers />
          <plotEquations>
            <plotEquation>
              <math>
                <apply xmlns="http://schemas.mathsoft.com/math50">
                  <mult />
                  <apply>
                    <id labels="FUNCTION" xml:space="preserve" label-is-contextual="true">I0</id>
                    <id labels="VARIABLE" xml:space="preserve" label-is-contextual="true">y</id>
                  </apply>
                  <apply>
                    <pow />
                    <id labels="CONSTANT" xml:space="preserve" label-is-contextual="true">e</id>
                    <apply>
                      <neg />
                      <apply>
                        <absval />
                        <id labels="VARIABLE" xml:space="preserve" label-is-contextual="true">y</id>
                      </apply>
                    </apply>
                  </apply>
                </apply>
              </math>
              <math>
                <placeholder xmlns="http://schemas.mathsoft.com/math50" />
              </math>
            </plotEquation>
            <plotEquation>
              <math>
                <apply xmlns="http://schemas.mathsoft.com/math50">
                  <id labels="FUNCTION" xml:space="preserve">I0.sc</id>
                  <id labels="VARIABLE" xml:space="preserve" label-is-contextual="true">y</id>
                </apply>
              </math>
              <math>
                <placeholder xmlns="http://schemas.mathsoft.com/math50" />
              </math>
            </plotEquation>
          </plotEquations>
          <xyDomain scale-type="linear" auto-scale="true">
            <startValue resultRef="87">
              <real xmlns="http://schemas.mathsoft.com/math50">0</real>
            </startValue>
            <secondTickValue resultRef="88">
              <real xmlns="http://schemas.mathsoft.com/math50">1</real>
            </secondTickValue>
            <endValue resultRef="89">
              <real xmlns="http://schemas.mathsoft.com/math50">2</real>
            </endValue>
          </xyDomain>
        </yAxis>
      </axes>
    </xyPlot>
  </plot>
</region>

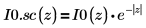
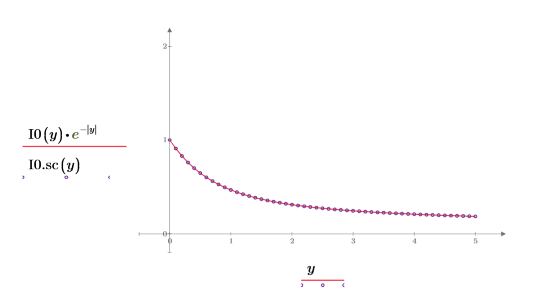
Las funciones modificadas de Bessel de primera especie no tienen picos.

Temas relacionados

Funciones modificadas de Bessel (hiperbólicas)

¿Fue esto útil?