Ejemplo: factorización de matrices QR
Utilice la función QR para realizar la factorización de matrices QR.
|
|
• Para evitar discrepancias lógicas al realizar comparaciones booleanas, active la opción Igualdad aproximada de la lista desplegable Opciones de cálculo.
• El ejemplo utiliza una matriz compleja como entrada, pero la función también acepta como entrada una matriz real.
|
Factorización de QR con giro
1. Defina una matriz real M1 de dimensiones m x n, de modo que m > n.
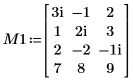
2. Defina el argumento p para controlar la activación/desactivación del giro.
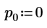
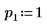
3. Utilice la función QR para realizar la factorización de matrices QR de la matriz M1.

La función por defecto QR(M1) es equivalente a QR(M,1).. 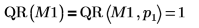 |
4. Muestre que M1 x P1 = Q1 x R1.
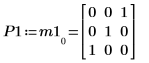


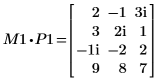 | 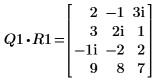 |
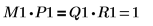 | |
La relación es lógicamente verdadera. | |
5. Utilice la función submatrix para extraer la matriz M2, de modo que m < n y, a continuación, aplique la función QR.
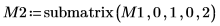
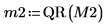
6. Muestre que M2 x P2 = Q2 x R2.
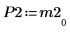 | 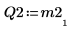 | 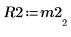 |
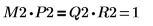 | ||
La relación es lógicamente verdadera. | ||
7. Utilice la función submatrix para extraer la matriz M3, de modo que m = n y, a continuación, aplique la función QR.
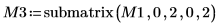
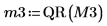
8. Muestre que M3 x P3 = Q3 x R3.
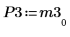 | 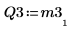 | 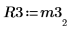 |
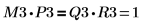 | ||
La relación es lógicamente verdadera. | ||
Factorización de QR sin giro
1. Desactive el giro y, a continuación, aplique la función QR a la matriz M1 (m > n).

2. Muestre que M1 = Q10 x R10.


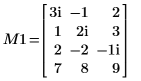 | 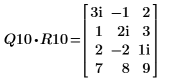 |
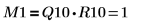 | |
La relación es lógicamente verdadera. | |
3. Desactive el giro y, a continuación, aplique la función QR a la matriz M2 (m < n).
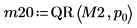
4. Muestre que M2 = Q20 x R20.
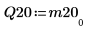 | 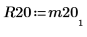 |
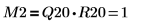 | |
La relación es lógicamente verdadera. | |
5. Desactive el giro y, a continuación, aplique la función QR a la matriz M3 (m = n).
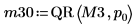
6. Muestre que M3 = Q30 x R30.
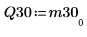 | 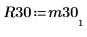 |
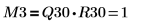 | |
La relación es lógicamente verdadera. | |