Ejemplo: métodos de predicción lineal
Utilice las funciones burg y yulew para generar coeficientes para el modelo de predicción lineal mencionado. Estas funciones implementan el método de Burg y el algoritmo de Yule-Walker, respectivamente. Para ver una descripción de estos algoritmos y los conceptos matemáticos detrás de ellos, consulte el libro Optimum Signal Processing, Sophocles J. Orfanidis, Macmillan (1989).
Predicción de Yule-Walker
1. Utilice la función cos para definir una señal de coseno.
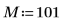
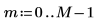
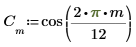
2. Trace la señal.
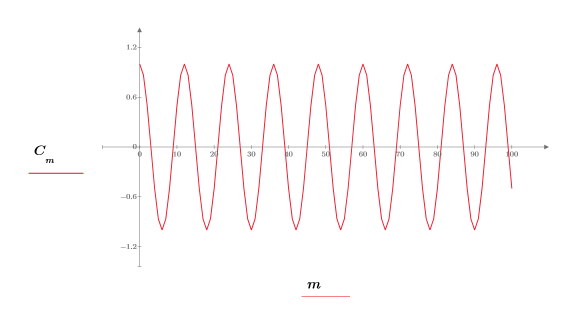
3. Utilice la función rnd para añadir ruido aleatorio a la señal.
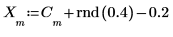
4. Trace las señales original y ruidosa.
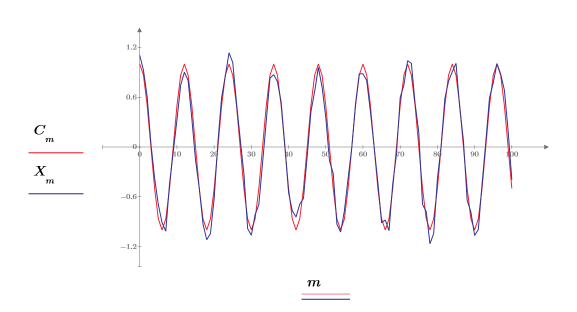
Se resta 0.2 de la señal para centrar el componente aleatorio alrededor de la amplitud 0.
5. Tome una pequeña muestra del principio de la señal.
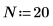
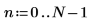
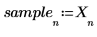
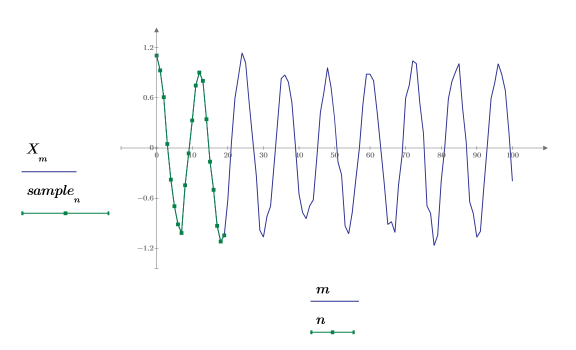
6. Defina el orden de predicción y utilice la función yulew para calcular los coeficientes.
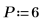
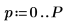

◦ Estos coeficientes son para un filtro de todos polos que se aproxima a la señal original. Tal como era de esperar, hay un polo grande, que representa al coseno, y varios polos más pequeños, que se aproximan al ruido.
◦ El orden P determina el número de valores consecutivos utilizados para predecir el siguiente valor de la secuencia. Se utilizan los seis primeros elementos del vector de coeficientes y se desestima el elemento cero, que siempre es 1. Este 1 es necesario cuando se utiliza y como filtro de errores de predicción para generar el conjunto completo de errores de predicción.
7. Compare los puntos previstos, calculados mediante los P puntos anteriores de la señal, con los datos originales. Esto demuestra el buen comportamiento que tendría el filtro si se utilizase en vez de la señal X.
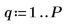
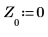
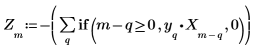
8. Trace la señal original y la prevista.
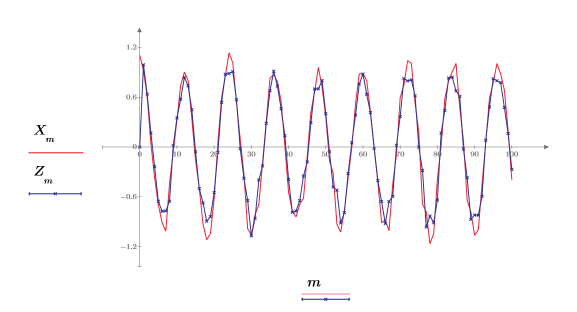
La aproximación es muy buena, aunque solo se utilicen los 20 primeros puntos de datos.
9. Utilice la función response para generar los errores de predicción de los coeficientes de Yule-Walker usando el array de coeficientes como filtro y calculando, a continuación, la respuesta con la muestra como entrada.
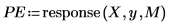
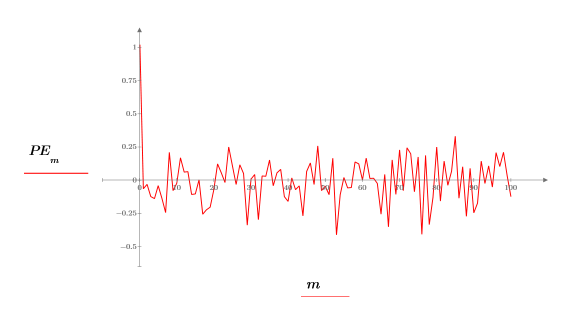
A veces, el array de coeficientes completo se conoce como filtro de errores de predicción.
10. Verifique que estos errores proporcionan realmente la diferencia entre los dos gráficos anteriores.
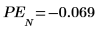
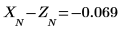
El algoritmo de Yule-Walker minimiza la suma de los cuadrados de los errores de predicción.
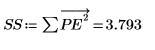
11. Verifique aleatoriamente la minimización perturbando y (añadiendo una pequeña cantidad aleatoria a todos los coeficientes excepto el primero) y volviendo a calcular la suma (colocando el cursor en la función rnd siguiente y pulsando [F5] varias veces).
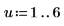
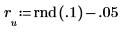
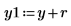
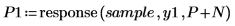
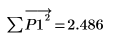
Predicción de Burg
1. Cree una secuencia cuya predicción lineal debe funcionar correctamente: un proceso autorregresivo con coeficientes conocidos.
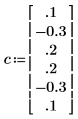
2. Inicialice las series temporales.
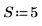
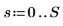
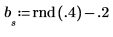
3. Genere el resto de las series mediante autorregresión más ruido.
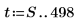
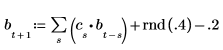
4. Tome como muestra toda la serie temporal y calcule los coeficientes para un modelo de orden 6 y, a continuación, utilice la función burg para calcular los coeficientes.
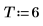
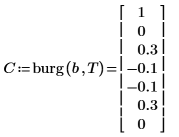
5. Compare los coeficientes generados por el proceso usando la convención de signos de este documento.
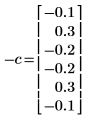
◦ El coeficiente cero se omitió, puesto que siempre es igual a uno.
◦ Los elementos calculados 1 y 5 de C son diferentes.
6. Utilice el vector de coeficientes de Burg C para generar los errores de predicción.
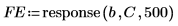
◦ El método de Burg asigna una ponderación 0 a los P primeros errores, de modo que la minimización no se ve afectada por el relleno con ceros de la muestra, como en el caso de la minimización realizada por Yule-Walker.
◦ El criterio de Burg también implica los errores directos FE y los errores inversos BE.
7. Utilice las funciones response y reverse para calcular los errores inversos.
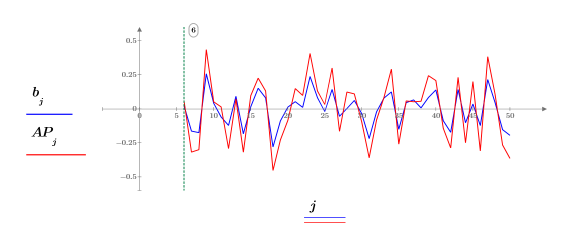
8. Utilice los errores de predicción FE y la función de autorregresión b para calcular las predicciones reales AP. A continuación, trace una parte de las series prevista y real, a partir del término Pth.
Cálculo aproximado espectral
Es posible utilizar los coeficientes generados por los métodos de predicción lineal para realizar un cálculo aproximado del espectro de potencia del proceso que se está modelando. En este contexto, el algoritmo de Burg se conoce como el análisis espectral de máxima entropía (MESA, maximum entropy spectrum analysis) y, en algunos casos, permite determinar los espectros de series temporales cortas con mayor precisión que FFT.
Haga un cálculo aproximado del espectro de potencia de un proceso que consista en la suma de sinusoides con ruido gaussiano añadido.
1. Utilice la función sin para definir una señal que tenga dos componentes de seno.
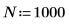
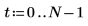
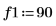
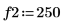
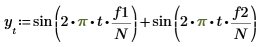
2. Utilice la función gaussn para añadir cierto ruido gaussiano.
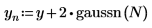
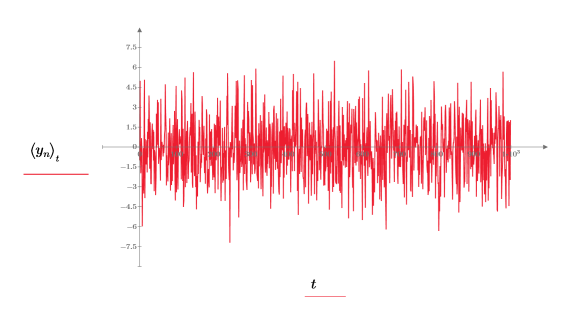
La función gaussn devuelve un vector de n elementos de números aleatorios tras una distribución de probabilidad gaussiana de media 0 y desviación estándar 1.
3. Defina dos órdenes para la predicción lineal.
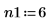
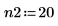
4. Utilice la función burg para realizar un cálculo aproximado del espectro con modelos autorregresivos de los dos órdenes usando la serie temporal en su totalidad como la muestra.
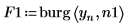
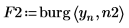
5. Utilice la función gain para calcular los espectros de potencia correspondientes, como la magnitud cuadrática de la función de transferencia definida por los arrays de coeficientes F1 y F2.
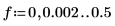
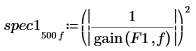
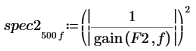
6. Trace los dos espectros de potencia.
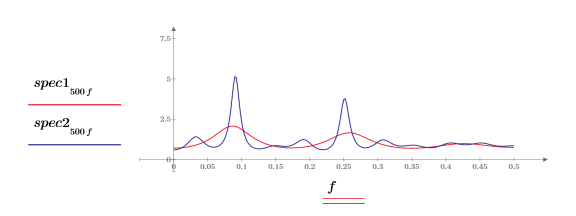
◦ Cada espectro de potencia tiene dos picos.
◦ Los picos de frecuencia inferior y superior para ambos espectros tienen lugar aproximadamente en la misma frecuencia.
7. Subdivida las curvas spec1 y spec2 en dos segmentos cada una para facilitar la búsqueda de sus picos de ganancia y las frecuencias en que se producen.
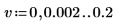 | 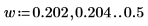 |
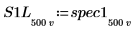 | 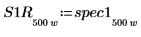 |
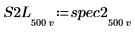 | 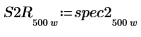 |
8. Utilice la función if para definir una función que devuelva la frecuencia en la que el segmento determinado tenga un pico y, a continuación, úsela para buscar los picos izquierdo y derecho de las trazas de cada espectro.
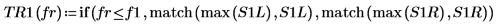 | |
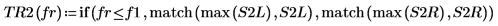 | |
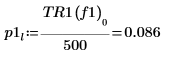 | 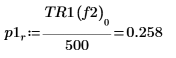 |
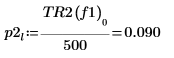 | 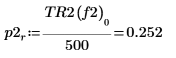 |
9. Utilice la función max para calcular la magnitud de cada pico.
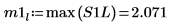 | 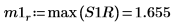 |
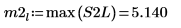 | 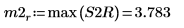 |
10. Trace cada función por separado. Utilice marcadores verticales y horizontales para mostrar la magnitud de cada pico y la frecuencia en la que se produce.
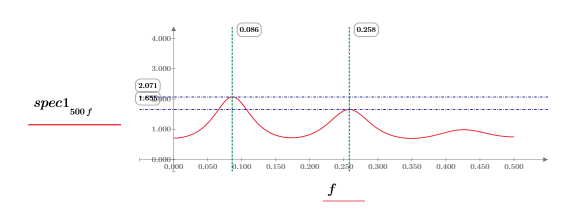
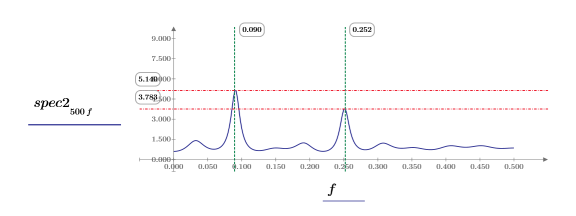
◦ Observe los dos gráficos al volver a calcular la hoja de trabajo.
◦ La magnitud de los picos varía con cada nuevo cálculo y normalmente tienen valores distintos. Sin embargo, es posible que las magnitudes sean iguales.
◦ Los picos se producen aproximadamente en las mismas frecuencias.
Para obtener más información sobre este método de cálculo aproximado del espectro, consulte Digital Spectral Analysis with Applications de S. Lawrence Marple, Jr. (Prentice-Hall, Inc.).