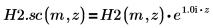Ejemplo: Funciones de Hankel de primera y segunda especie

Funciones > Funciones especiales > Funciones de Bessel > Ejemplo: Funciones de Hankel de primera y segunda especie

Muestre la relación entre las funciones de Hankel H1 y H2 con las funciones de Bessel Jn e Yn. Muestre también las relaciones entre estas funciones y sus versiones escaladas.

Las funciones de Hankel no se definen en 0.

1. Utilice la evaluación simbólica para mostrar la relación entre H1, Jn e Yn.

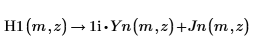
2. Utilice la evaluación simbólica para mostrar la relación entre H2, Jn e Yn.

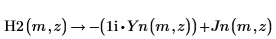
◦ Los componentes reales de H1 y H2 son idénticos en valor y signo.

◦ Los componentes imaginarios de H1 y H2 son idénticos en valor, pero opuestos en signo.

3. Observe estas otras dos relaciones destacadas entre H1 y H2.

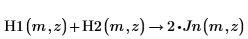
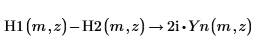
4. Cree un gráfico para mostrar visualmente esa relación |H1|=|H2|.

<region id="ID0EV6Y6" actualWidth="571.66857242138985" actualHeight="316.8" top="192.00000000000003" left="0" height="316.8" width="571.66857242138985" xmlns="http://schemas.mathsoft.com/worksheet50">
  <plot background-type="white" origin-positioning="true">
    <xyPlot>
      <title class="- topic/title " wwtype:type="Paragraph" xmlns:wwtype="urn:WebWorks-Type-Schema" />
      <legend />
      <traces>
        <trace resultRef="33">
          <traceStyle color="#FFED1D2F" symbol="none" line-weight="1" line-style="Solid">lines</traceStyle>
        </trace>
        <trace resultRef="34">
          <traceStyle color="#FF0000FF" symbol="none" line-weight="1" line-style="Dash">lines</traceStyle>
        </trace>
      </traces>
      <graph-size width="418.06857242139" height="259.2" />
      <axes>
        <xAxis rank="1" legend-position="PlotBoundaryBottom" start="0" end="20">
          <axisLine position="origin" positionticmark="0" legendWidth="60.93" />
          <axisGrid>
            <gridFrequency>11</gridFrequency>
            <gridLabels display="true" />
            <gridLines />
            <tickMarks display="true" />
          </axisGrid>
          <axisLabel />
          <markers />
          <plotEquations>
            <plotEquation>
              <math>
                <id labels="VARIABLE" label-is-contextual="true" xml:space="preserve" xmlns="http://schemas.mathsoft.com/math50">x</id>
              </math>
              <math>
                <placeholder xmlns="http://schemas.mathsoft.com/math50" />
              </math>
            </plotEquation>
          </plotEquations>
          <xyDomain scale-type="linear" auto-scale="true">
            <startValue>
              <placeholder xmlns="http://schemas.mathsoft.com/math50" />
            </startValue>
            <endValue>
              <placeholder xmlns="http://schemas.mathsoft.com/math50" />
            </endValue>
          </xyDomain>
        </xAxis>
        <yAxis rank="1" legend-position="PlotBoundaryLeft" start="0" end="2">
          <axisLine position="origin" positionticmark="0" legendWidth="125.873333333333" />
          <axisGrid>
            <gridFrequency>5</gridFrequency>
            <gridLabels display="true" />
            <gridLines />
            <tickMarks display="true" />
          </axisGrid>
          <axisLabel />
          <markers />
          <plotEquations>
            <plotEquation>
              <math>
                <apply xmlns="http://schemas.mathsoft.com/math50">
                  <absval />
                  <apply>
                    <id labels="FUNCTION" xml:space="preserve">H1</id>
                    <sequence>
                      <id labels="VARIABLE" label-is-contextual="true" xml:space="preserve">m</id>
                      <id labels="VARIABLE" label-is-contextual="true" xml:space="preserve">x</id>
                    </sequence>
                  </apply>
                </apply>
              </math>
              <math>
                <placeholder xmlns="http://schemas.mathsoft.com/math50" />
              </math>
            </plotEquation>
            <plotEquation>
              <math>
                <apply xmlns="http://schemas.mathsoft.com/math50">
                  <absval />
                  <apply>
                    <id labels="FUNCTION" label-is-contextual="true" xml:space="preserve">H2</id>
                    <sequence>
                      <id labels="VARIABLE" label-is-contextual="true" xml:space="preserve">m</id>
                      <id labels="VARIABLE" label-is-contextual="true" xml:space="preserve">x</id>
                    </sequence>
                  </apply>
                </apply>
              </math>
              <math>
                <placeholder xmlns="http://schemas.mathsoft.com/math50" />
              </math>
            </plotEquation>
          </plotEquations>
          <xyDomain scale-type="linear" auto-scale="true">
            <startValue resultRef="35">
              <real xmlns="http://schemas.mathsoft.com/math50">0</real>
            </startValue>
            <secondTickValue resultRef="36">
              <real xmlns="http://schemas.mathsoft.com/math50">0.5</real>
            </secondTickValue>
            <endValue>
              <placeholder xmlns="http://schemas.mathsoft.com/math50" />
            </endValue>
          </xyDomain>
        </yAxis>
      </axes>
    </xyPlot>
  </plot>
</region>

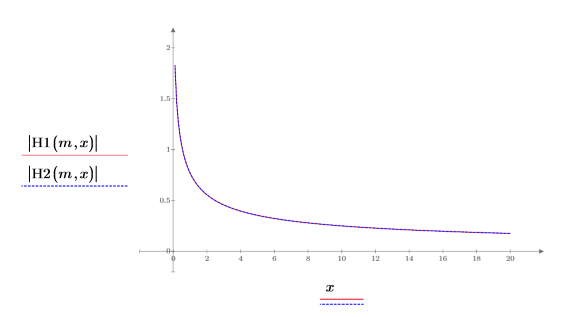
5. Cree un gráfico para mostrar la relación entre H1, Jn e Yn.

<region id="ID0ERBZ6" actualWidth="571.66857242139008" actualHeight="336" top="518.40000000000009" left="0" height="336" width="571.66857242139008" xmlns="http://schemas.mathsoft.com/worksheet50">
  <plot background-type="white" origin-positioning="true">
    <xyPlot>
      <title class="- topic/title " wwtype:type="Paragraph" xmlns:wwtype="urn:WebWorks-Type-Schema" />
      <legend />
      <traces>
        <trace resultRef="37">
          <traceStyle color="#FFED1D2F" symbol="none" line-weight="1" line-style="Dash">lines</traceStyle>
        </trace>
        <trace resultRef="38">
          <traceStyle color="#FF068149" symbol="none" line-weight="1" line-style="Solid">lines</traceStyle>
        </trace>
        <trace resultRef="39">
          <traceStyle color="#FF2E3192" symbol="none" line-weight="1" line-style="Solid">lines</traceStyle>
        </trace>
      </traces>
      <graph-size width="418.06857242139" height="259.2" />
      <axes>
        <xAxis rank="1" legend-position="PlotBoundaryBottom" start="0" end="20">
          <axisLine position="origin" positionticmark="2" legendWidth="60.93" />
          <axisGrid>
            <gridFrequency>11</gridFrequency>
            <gridLabels display="true" />
            <gridLines />
            <tickMarks display="true" />
          </axisGrid>
          <axisLabel />
          <markers />
          <plotEquations>
            <plotEquation>
              <math>
                <id labels="VARIABLE" label-is-contextual="true" xml:space="preserve" xmlns="http://schemas.mathsoft.com/math50">x</id>
              </math>
              <math>
                <placeholder xmlns="http://schemas.mathsoft.com/math50" />
              </math>
            </plotEquation>
          </plotEquations>
          <xyDomain scale-type="linear" auto-scale="true">
            <startValue>
              <placeholder xmlns="http://schemas.mathsoft.com/math50" />
            </startValue>
            <endValue>
              <placeholder xmlns="http://schemas.mathsoft.com/math50" />
            </endValue>
          </xyDomain>
        </xAxis>
        <yAxis rank="1" legend-position="PlotBoundaryLeft" start="-1" end="2">
          <axisLine position="origin" positionticmark="0" legendWidth="125.873333333333" />
          <axisGrid>
            <gridFrequency>7</gridFrequency>
            <gridLabels display="true" />
            <gridLines />
            <tickMarks display="true" />
          </axisGrid>
          <axisLabel />
          <markers />
          <plotEquations>
            <plotEquation>
              <math>
                <apply xmlns="http://schemas.mathsoft.com/math50">
                  <absval />
                  <apply>
                    <id labels="FUNCTION" xml:space="preserve">H1</id>
                    <sequence>
                      <id labels="VARIABLE" label-is-contextual="true" xml:space="preserve">m</id>
                      <id labels="VARIABLE" label-is-contextual="true" xml:space="preserve">x</id>
                    </sequence>
                  </apply>
                </apply>
              </math>
              <math>
                <placeholder xmlns="http://schemas.mathsoft.com/math50" />
              </math>
            </plotEquation>
            <plotEquation>
              <math>
                <apply xmlns="http://schemas.mathsoft.com/math50">
                  <id labels="FUNCTION" xml:space="preserve">Jn</id>
                  <sequence>
                    <id labels="VARIABLE" label-is-contextual="true" xml:space="preserve">m</id>
                    <id labels="VARIABLE" label-is-contextual="true" xml:space="preserve">x</id>
                  </sequence>
                </apply>
              </math>
              <math>
                <placeholder xmlns="http://schemas.mathsoft.com/math50" />
              </math>
            </plotEquation>
            <plotEquation>
              <math>
                <apply xmlns="http://schemas.mathsoft.com/math50">
                  <id labels="FUNCTION" label-is-contextual="true" xml:space="preserve">Yn</id>
                  <sequence>
                    <id labels="VARIABLE" label-is-contextual="true" xml:space="preserve">m</id>
                    <id labels="VARIABLE" label-is-contextual="true" xml:space="preserve">x</id>
                  </sequence>
                </apply>
              </math>
              <math>
                <placeholder xmlns="http://schemas.mathsoft.com/math50" />
              </math>
            </plotEquation>
          </plotEquations>
          <xyDomain scale-type="linear" auto-scale="true">
            <startValue resultRef="40">
              <real xmlns="http://schemas.mathsoft.com/math50">-1</real>
            </startValue>
            <secondTickValue resultRef="41">
              <real xmlns="http://schemas.mathsoft.com/math50">-0.5</real>
            </secondTickValue>
            <endValue>
              <placeholder xmlns="http://schemas.mathsoft.com/math50" />
            </endValue>
          </xyDomain>
        </yAxis>
      </axes>
    </xyPlot>
  </plot>
</region>

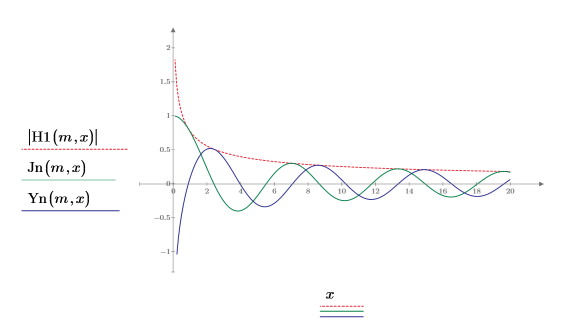
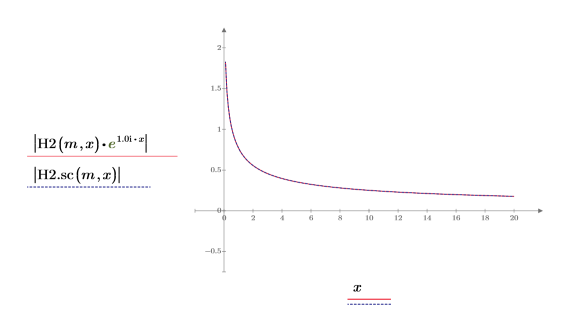
6. Utilice la evaluación simbólica para mostrar la relación entre las funciones de Hankel y su versión escalada.

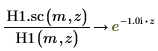
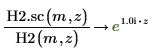
7. Cree un gráfico para mostrar que:

<region id="ID0ENFZ6" actualWidth="571.2685724213901" actualHeight="316.8" top="1017.6000000000001" left="0" height="316.8" width="571.2685724213901" xmlns="http://schemas.mathsoft.com/worksheet50">
  <plot background-type="white" origin-positioning="true">
    <xyPlot>
      <title class="- topic/title " wwtype:type="Paragraph" xmlns:wwtype="urn:WebWorks-Type-Schema" />
      <legend />
      <traces>
        <trace resultRef="45">
          <traceStyle color="#FFED1D2F" symbol="none" line-weight="1" line-style="Solid">lines</traceStyle>
        </trace>
        <trace resultRef="46">
          <traceStyle color="#FF2E3192" symbol="none" line-weight="1" line-style="Dash">lines</traceStyle>
        </trace>
      </traces>
      <graph-size width="360.06857242139" height="259.2" />
      <axes>
        <xAxis rank="1" legend-position="PlotBoundaryBottom" start="0" end="20">
          <axisLine position="origin" positionticmark="1" legendWidth="60.93" />
          <axisGrid>
            <gridFrequency>11</gridFrequency>
            <gridLabels display="true" />
            <gridLines />
            <tickMarks display="true" />
          </axisGrid>
          <axisLabel />
          <markers />
          <plotEquations>
            <plotEquation>
              <math>
                <id labels="VARIABLE" label-is-contextual="true" xml:space="preserve" xmlns="http://schemas.mathsoft.com/math50">x</id>
              </math>
              <math>
                <placeholder xmlns="http://schemas.mathsoft.com/math50" />
              </math>
            </plotEquation>
          </plotEquations>
          <xyDomain scale-type="linear" auto-scale="true">
            <startValue>
              <placeholder xmlns="http://schemas.mathsoft.com/math50" />
            </startValue>
            <endValue>
              <placeholder xmlns="http://schemas.mathsoft.com/math50" />
            </endValue>
          </xyDomain>
        </xAxis>
        <yAxis rank="1" legend-position="PlotBoundaryLeft" start="-0.5" end="2">
          <axisLine position="origin" positionticmark="0" legendWidth="178.54" />
          <axisGrid>
            <gridFrequency>6</gridFrequency>
            <gridLabels display="true" />
            <gridLines />
            <tickMarks display="true" />
          </axisGrid>
          <axisLabel />
          <markers />
          <plotEquations>
            <plotEquation>
              <math>
                <apply xmlns="http://schemas.mathsoft.com/math50">
                  <absval />
                  <apply>
                    <mult />
                    <apply>
                      <id labels="FUNCTION" xml:space="preserve">H1</id>
                      <sequence>
                        <id labels="VARIABLE" label-is-contextual="true" xml:space="preserve">m</id>
                        <id labels="VARIABLE" label-is-contextual="true" xml:space="preserve">x</id>
                      </sequence>
                    </apply>
                    <apply>
                      <pow />
                      <id labels="CONSTANT" label-is-contextual="true" xml:space="preserve">e</id>
                      <apply>
                        <mult />
                        <imag symbol="i">-1.0</imag>
                        <id labels="VARIABLE" label-is-contextual="true" xml:space="preserve">x</id>
                      </apply>
                    </apply>
                  </apply>
                </apply>
              </math>
              <math>
                <placeholder xmlns="http://schemas.mathsoft.com/math50" />
              </math>
            </plotEquation>
            <plotEquation>
              <math>
                <apply xmlns="http://schemas.mathsoft.com/math50">
                  <absval />
                  <apply>
                    <id labels="FUNCTION" label-is-contextual="true" xml:space="preserve">H1.sc</id>
                    <sequence>
                      <id labels="VARIABLE" label-is-contextual="true" xml:space="preserve">m</id>
                      <id labels="VARIABLE" label-is-contextual="true" xml:space="preserve">x</id>
                    </sequence>
                  </apply>
                </apply>
              </math>
              <math>
                <placeholder xmlns="http://schemas.mathsoft.com/math50" />
              </math>
            </plotEquation>
          </plotEquations>
          <xyDomain scale-type="linear" auto-scale="true">
            <startValue resultRef="47">
              <real xmlns="http://schemas.mathsoft.com/math50">-0.5</real>
            </startValue>
            <secondTickValue resultRef="48">
              <real xmlns="http://schemas.mathsoft.com/math50">0</real>
            </secondTickValue>
            <endValue>
              <placeholder xmlns="http://schemas.mathsoft.com/math50" />
            </endValue>
          </xyDomain>
        </yAxis>
      </axes>
    </xyPlot>
  </plot>
</region>

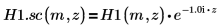
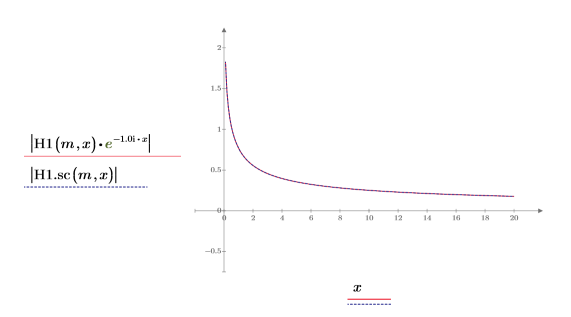
8. Cree un gráfico para mostrar que:

<region id="ID0ELHZ6" actualWidth="571.26857242139" actualHeight="316.8" top="1382.4" left="0" height="316.8" width="571.26857242139" xmlns="http://schemas.mathsoft.com/worksheet50">
  <plot background-type="white" origin-positioning="true">
    <xyPlot>
      <title class="- topic/title " wwtype:type="Paragraph" xmlns:wwtype="urn:WebWorks-Type-Schema" />
      <legend />
      <traces>
        <trace resultRef="50">
          <traceStyle color="#FFED1D2F" symbol="none" line-weight="1" line-style="Solid">lines</traceStyle>
        </trace>
        <trace resultRef="51">
          <traceStyle color="#FF2E3192" symbol="none" line-weight="1" line-style="Dash">lines</traceStyle>
        </trace>
      </traces>
      <graph-size width="360.06857242139" height="259.2" />
      <axes>
        <xAxis rank="1" legend-position="PlotBoundaryBottom" start="0" end="20">
          <axisLine position="origin" positionticmark="1" legendWidth="60.93" />
          <axisGrid>
            <gridFrequency>11</gridFrequency>
            <gridLabels display="true" />
            <gridLines />
            <tickMarks display="true" />
          </axisGrid>
          <axisLabel />
          <markers />
          <plotEquations>
            <plotEquation>
              <math>
                <id labels="VARIABLE" label-is-contextual="true" xml:space="preserve" xmlns="http://schemas.mathsoft.com/math50">x</id>
              </math>
              <math>
                <placeholder xmlns="http://schemas.mathsoft.com/math50" />
              </math>
            </plotEquation>
          </plotEquations>
          <xyDomain scale-type="linear" auto-scale="true">
            <startValue>
              <placeholder xmlns="http://schemas.mathsoft.com/math50" />
            </startValue>
            <endValue>
              <placeholder xmlns="http://schemas.mathsoft.com/math50" />
            </endValue>
          </xyDomain>
        </xAxis>
        <yAxis rank="1" legend-position="PlotBoundaryLeft" start="-0.5" end="2">
          <axisLine position="origin" positionticmark="0" legendWidth="171.7" />
          <axisGrid>
            <gridFrequency>6</gridFrequency>
            <gridLabels display="true" />
            <gridLines />
            <tickMarks display="true" />
          </axisGrid>
          <axisLabel />
          <markers />
          <plotEquations>
            <plotEquation>
              <math>
                <apply xmlns="http://schemas.mathsoft.com/math50">
                  <absval />
                  <apply>
                    <mult />
                    <apply>
                      <id labels="FUNCTION" xml:space="preserve">H2</id>
                      <sequence>
                        <id labels="VARIABLE" label-is-contextual="true" xml:space="preserve">m</id>
                        <id labels="VARIABLE" label-is-contextual="true" xml:space="preserve">x</id>
                      </sequence>
                    </apply>
                    <apply>
                      <pow />
                      <id labels="CONSTANT" label-is-contextual="true" xml:space="preserve">e</id>
                      <apply>
                        <mult />
                        <imag symbol="i">1.0</imag>
                        <id labels="VARIABLE" label-is-contextual="true" xml:space="preserve">x</id>
                      </apply>
                    </apply>
                  </apply>
                </apply>
              </math>
              <math>
                <placeholder xmlns="http://schemas.mathsoft.com/math50" />
              </math>
            </plotEquation>
            <plotEquation>
              <math>
                <apply xmlns="http://schemas.mathsoft.com/math50">
                  <absval />
                  <apply>
                    <id labels="FUNCTION" label-is-contextual="true" xml:space="preserve">H2.sc</id>
                    <sequence>
                      <id labels="VARIABLE" label-is-contextual="true" xml:space="preserve">m</id>
                      <id labels="VARIABLE" label-is-contextual="true" xml:space="preserve">x</id>
                    </sequence>
                  </apply>
                </apply>
              </math>
              <math>
                <placeholder xmlns="http://schemas.mathsoft.com/math50" />
              </math>
            </plotEquation>
          </plotEquations>
          <xyDomain scale-type="linear" auto-scale="true">
            <startValue resultRef="52">
              <real xmlns="http://schemas.mathsoft.com/math50">-0.5</real>
            </startValue>
            <secondTickValue resultRef="53">
              <real xmlns="http://schemas.mathsoft.com/math50">0</real>
            </secondTickValue>
            <endValue>
              <placeholder xmlns="http://schemas.mathsoft.com/math50" />
            </endValue>
          </xyDomain>
        </yAxis>
      </axes>
    </xyPlot>
  </plot>
</region>

Temas relacionados

Funciones de Hankel

¿Fue esto útil?