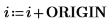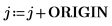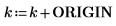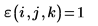Ejemplo: Efecto de ORIGEN en las funciones que no son de búsqueda
La variable del sistema ORIGIN afecta al resultado de las tres funciones que se aplican a las arrays: submatrix, csort y rsort.
También afecta a una función que no opera en arrays: e (la función de tensor antisimétrico).
1. Defina una matriz de entrada.

2. Evalúe ORIGIN para garantizar que esté definida en 0.
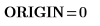
ORIGEN = 0: submatrix, csort y rsort
1. Defina los argumentos de fila y columna.
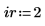
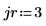
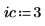
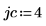
2. Utilice la función submatrix para extraer una submatriz de la matriz M.
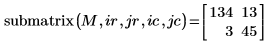
El resultado es la submatriz que se encuentra entre las filas 2 y 3, y las columnas 3 y 4.
3. Defina el argumento de columna y evalúe la función de clasificación de columna csort.
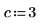

La matriz devuelta es el resultado de reorganizar las filas de M hasta que la columna 3 está en orden ascendente.
4. Defina el argumento de fila y evalúe la función de clasificación de fila rsort.
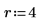

La matriz devuelta es el resultado de reorganizar las columnas de M hasta que la fila 4 está en orden ascendente.
ORIGEN = 1: submatrix, csort y rsort
1. Defina ORIGIN en 1.
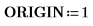
2. Vuelva a evaluar la función submatrix.
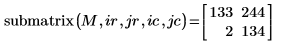
La matriz devuelta ahora procede de las filas 1 y 2, y las columnas 2 y 3.
3. Muestre que, con el fin de obtener los mismos resultados cuando ORIGIN se defina en 0, debe añadir el nuevo valor de ORIGIN a los índices de fila y columna de la función submatrix.
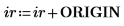
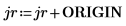
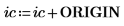
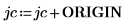
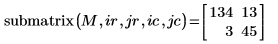
4. Vuelva a evaluar la función csort.

La matriz devuelta muestra ahora que la columna 2, y no la 3, está en orden ascendente.
5. Muestre que, con el fin de obtener los mismos resultados cuando ORIGIN se defina en 0, debe añadir el nuevo valor de ORIGIN al argumento c.
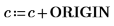

6. Vuelva a evaluar la función rsort.

La matriz devuelta muestra que la fila 3, y no la 4, está en orden ascendente.
7. Muestre que, con el fin de obtener los mismos resultados cuando ORIGIN se defina en 0, debe añadir el nuevo valor de ORIGIN al argumento r.
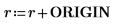

ORIGEN=0: e
1. Defina ORIGIN en 0.
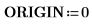
2. Defina los tres argumentos de la función de tensor antisimétrico: i, j y k.
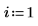
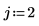
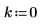
3. Evalúe la función antisymmetric tensor ε.
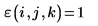
ORIGEN=1: e
1. Defina ORIGIN en 1.
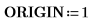
2. Vuelva a evaluar la función de tensor antisimétrico.
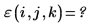
El error se produce porque el valor de cada argumento debe estar entre ORIGIN y ORIGIN+ 2.
3. Muestre que, con el fin de obtener los mismos resultados cuando ORIGIN se defina en 0, debe añadir el nuevo valor de ORIGIN a caca uno de los tres argumentos.