Ejemplo: transformada de coseno discreta
Utilice las funciones dct e idct para calcular la transformada discreta del coseno y la transformada inversa, respectivamente. Esta transformada tiene la ventaja de que concentra la mayoría de la "energía" o información de la imagen en unos pocos componentes de frecuencia, de modo que es una buena opción para la codificación.
Para obtener información sobre el uso de este ejemplo, consulte Acerca de los ejemplos de procesamiento de imágenes
1. Defina una matriz M de tamaño N x P.
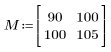
 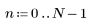 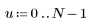 | 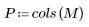 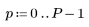 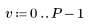 |
2. La implementación de la transformada de coseno utiliza la transformada de coseno discreta (DCT) de tipo II. Defina DCT como una fórmula analítica para esta transformada.
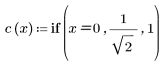
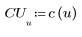
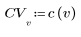
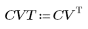
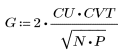
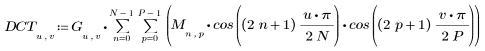
3. Evalúe la matriz DCT.
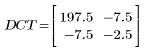
4. Aplique la función dct a la matriz M.
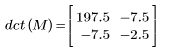
5. Calcule el error máximo entre la DCT y la función dct.
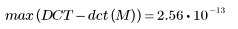
Compactación de energía
La transformada de coseno tiene excelentes propiedades de compactación de energía, lo que significa que concentra casi toda la energía en los primeros coeficientes de la transformada.
1. Defina una matriz de entrada.
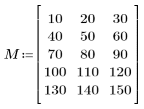
2. Aplique la función dct a la matriz M y evalúela.
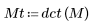
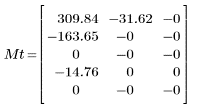
La matriz resultante muestra que la mayoría de la energía, relacionada con los valores del coeficiente, se concentra en los primeros elementos.
idct
La función inversa se utiliza para recuperar una imagen original a partir de su transformada.
1. Lea una versión en blanco y negro de la Mona Lisa.
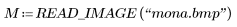

(mona.bmp)
2. Aplique la función dct para transformar la imagen.
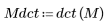


(mona_noise.bmp)
3. Aplique la función inversa para recuperar la imagen.
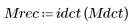


(mona_rec.bmp)
4. Verifique la propiedad de compactación de energía de la transformada de coseno discreta (DCT) en los histogramas de las imágenes transformada y original.
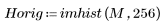
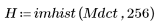
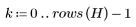
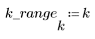
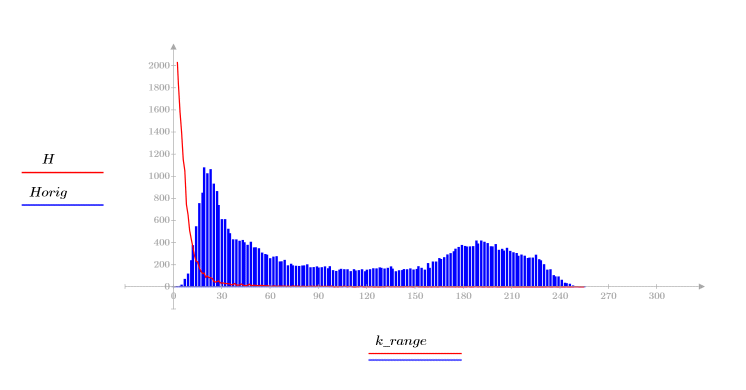
La imagen transformada concentra la mayoría de la energía en los primeros contenedores del histograma, mientras que la imagen original presenta una distribución dispersa. Por este motivo, la imagen transformada es un mejor candidato para la codificación o transmisión, ya que permite transmitir casi toda la información de la imagen con muy pocos componentes de frecuencia. Por eso se utiliza la transformada de coseno discreta (DCT) para comprimir las imágenes.