Ejemplo: Anulación de alianza de factores
Utilice las funciones fractfact, fractresol, fractruns, fractalias, quickscreen, effectsgraph, foldover y stack para filtrar los factores de un experimento que estudia el tiempo que necesita el ojo para enfocar. Los factores elegidos para el experimento son los siguientes:
|
A:
|
agudeza de la visión
|
|
B:
|
distancia entre el ojo y el objetivo
|
|
C:
|
forma del objetivo
|
|
D:
|
nivel de iluminación
|
|
E:
|
tamaño del objetivo
|
|
F:
|
densidad
|
|
G:
|
sujeto
|
Se supone que solo son importantes algunos factores y que se pueden obviar las interacciones de orden elevado entre los factores.
1. Defina el número de factores del experimento.
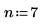
2. Defina la potencia fraccional de un diseño factorial fraccional.
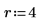
3. Llame a fractfact para crear la matriz de diseño X.
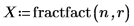
4. Defina la cadena gen para registrar los factores y el aliasing de la matriz de diseño X.
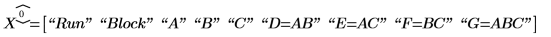
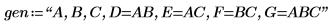
5. Llame a fractresol y fractruns para averiguar la resolución y el número de ejecuciones de la matriz de diseño X.
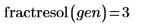
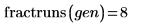
La matriz de diseño X representa una factorial fraccional de 8 ejecuciones de resolución III (sus factores principales no están asociados entre sí, pero están asociados con interacciones de segundo orden).
6. Registre los resultados del experimento en la matriz Y1 con una fila por ejecución y una columna por réplica.

7. Llame a la función quickscreen.

8. Llame a la función effectsgraph para crear un gráfico de efectos y determinar los factores que son significativos.
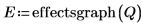

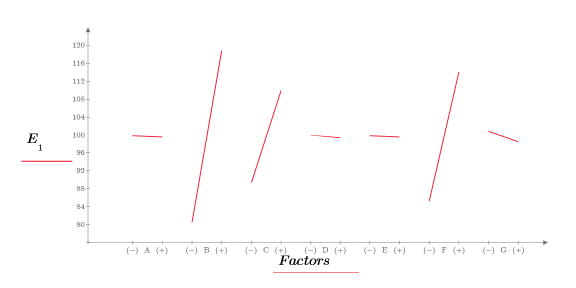
Los factores B, C y F presentan efectos importantes.
9. Llame a fractalias para averiguar las interacciones de segundo orden que están asociadas con B, C y F.
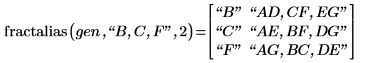
Si B y C son factores importantes, hay muchas probabilidades de que la interacción BC también sea importante. BC está asociado con F y no se sabe si el efecto apreciado en F está provocado por F o por BC. Este mismo problema se presenta para B y F, y para C y F. Hay que anular el alias de los factores principales y las interacciones de segundo orden.
10. Llame a foldover para duplicar la matriz de diseño X y anular los alias entre los factores principales y las interacciones de segundo orden.
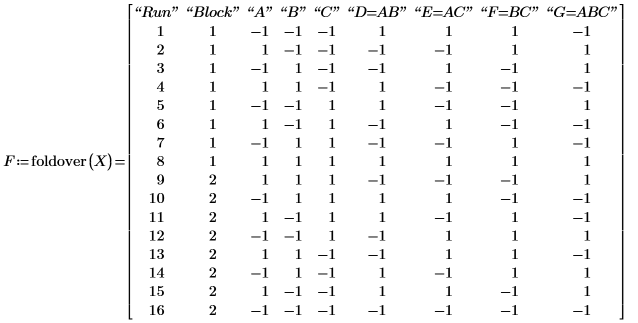
Las ocho filas de la matriz X se invierten en la mitad inferior de F. Se pueden elegir los factores específicos que deben duplicarse.
11. Registre los resultados de las ejecuciones adicionales de la matriz de diseño duplicada F.

12. Utilice la función de agrupación para agrupar las ejecuciones original y adicionales en la matriz Y.
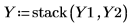
13. Llame a las funciones quickscreen y effectsgraph para crear un gráfico de efectos y determinar los efectos del factor.

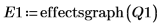
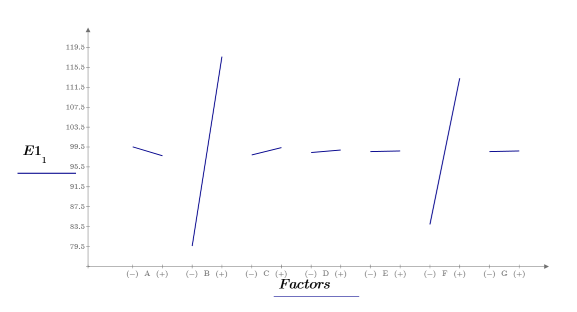
Solo son significativos los factores B y F. El efecto anterior apreciado para el factor C se debía a la interacción BF. Ahora se pueden realizar más experimentos para analizar el efecto del factor B (distancia entre el objetivo y el ojo) y el factor F (densidad) en el tiempo de enfoque.
Referencia
Montgomery, D.C., Design and Analysis of Experiments, 5th ed, John Wiley & Sons, Nueva York, 2001, pág. 341.