Ejemplo: cepstrum y cepstrum complejo
Utilice las funciones cepstrum y ccepstrum para calcular el cepstrum y el cepstrum complejo de una señal multicanal con valores reales.
El cepstrum asigna convolución y deconvolución a la suma y la sustracción del dominio de frecuencias. Además, tiene aplicaciones en el procesamiento de señales geofísicas y de voz.
cepstrum
El cepstrum de la secuencia x(n) se obtiene con la siguiente fórmula:
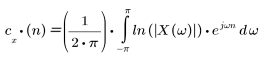
donde X(ω) es la transformada de Fourier de la secuencia x(n).
Esta es la definición de la transformada inversa tras aplicar un logaritmo natural a la transformada de Fourier de x(n). El logaritmo asigna la convolución del dominio del tiempo a la suma del dominio de frecuencias, de modo que cepstrum es una herramienta práctica para la deconvolución de señales, que se asigna a la sustracción.
1. Defina el rango de n.
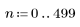
2. Defina la función de secuencia x.
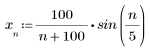
3. Trace la función de secuencia x.
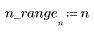
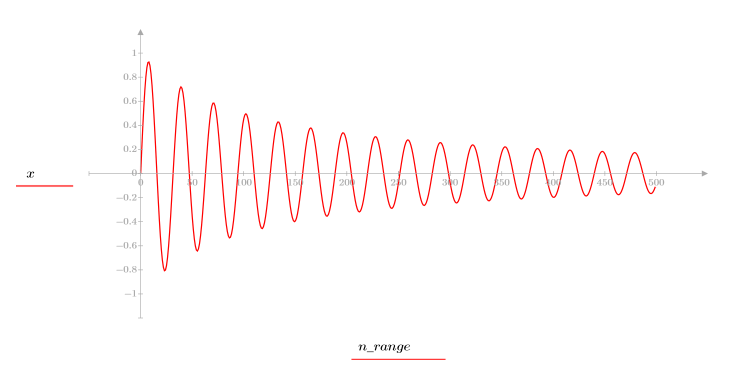
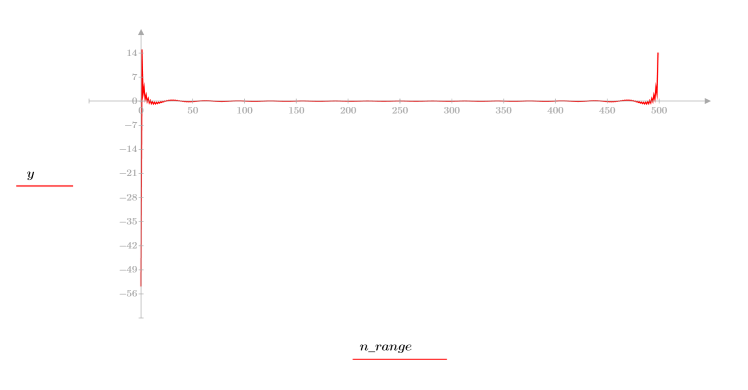
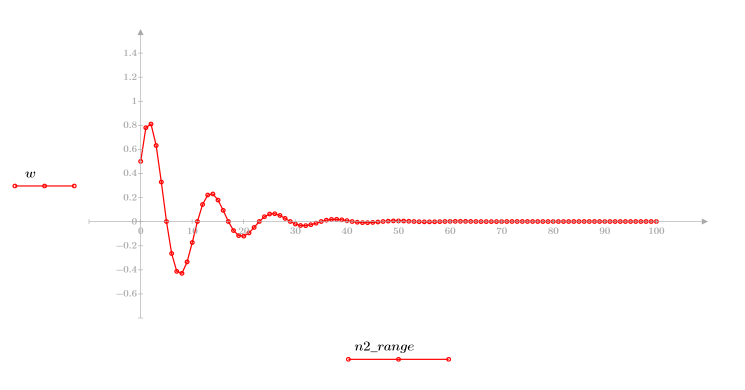
4. Calcule el cepstrum y trace la función resultante.
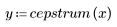
5. Utilice la función recenter para recentrar el resultado y colocar el primer elemento en el centro.
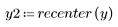
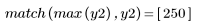
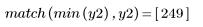
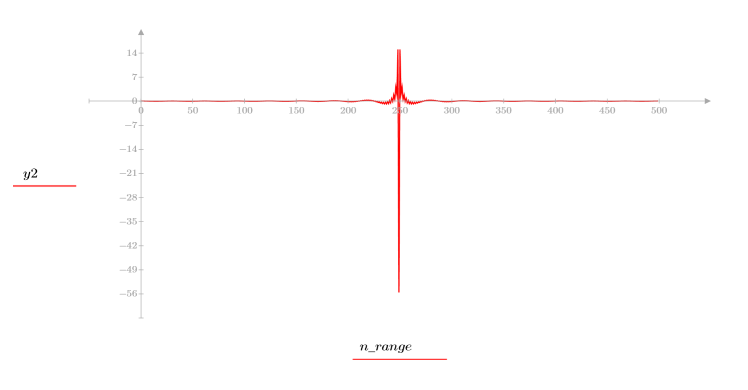
La señal original no se puede recuperar desde el cepstrum, ya que no se retiene la información de fase.
ccepstrum
La función del cepstrum complejo se obtiene con el logaritmo complejo siguiente.
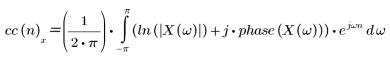
donde: X(ω) es la transformada de Fourier de la secuencia x(n) y fase se utiliza para capturar la información de fase de la secuencia especificada.
Al comparar el ccepstrum de la señal de salida con los de las secuencias de entrada y canal, se comprueba que el ccepstrum de la salida es la suma del ccepstrum de la entrada y el canal. Esto es similar a la suma de los espectros de dos señales del dominio de frecuencias, con la diferencia de que se hace en el dominio de tiempo.
En el ejemplo siguiente se simula una señal que pasa por un canal de comunicación que introduce ecos (según la sección 12.8.1 del libro de Oppenheim y Schaefer, Prentice-Hall, 1989).
1. Defina y trace la respuesta de canal como un filtro FIR que introduce copias atenuadas de otra secuencia (ecos).
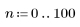
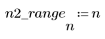
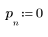
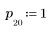
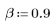
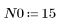
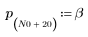
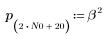
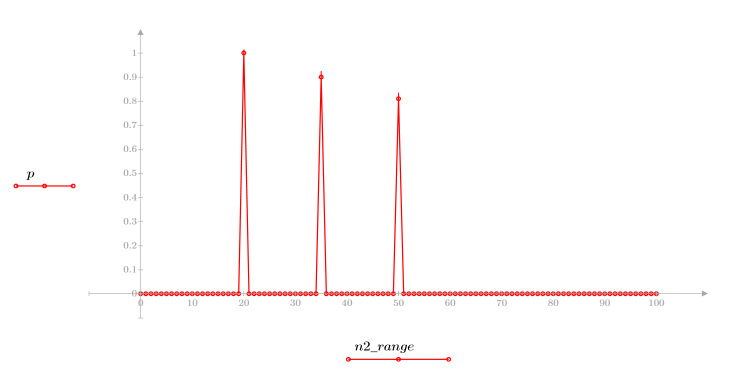
2. Defina y trace la secuencia v que se combinará con el canal de respuesta.
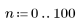
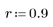
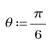
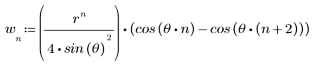
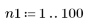
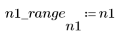
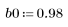
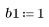
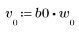
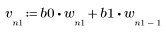
3. Utilice la función response para obtener la respuesta del vector del término n del vector de entrada p a un filtro FIR con un array de coeficientes v (la función del canal de comunicación v).
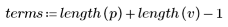
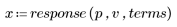
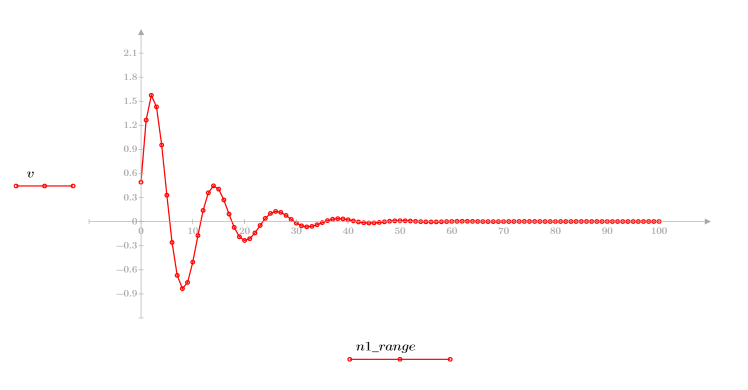
4. Trace la función de respuesta.
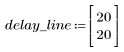
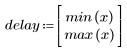
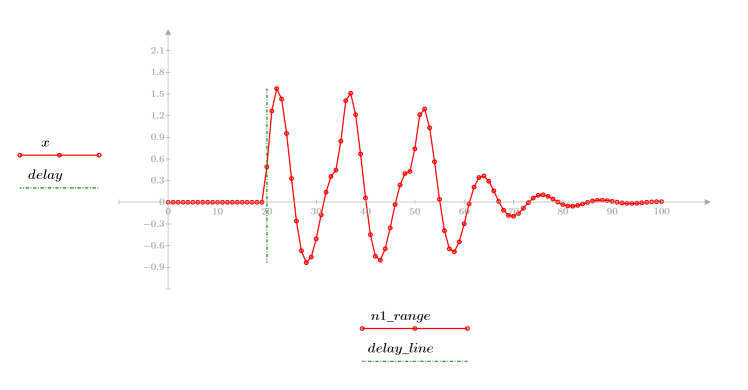
◦ La secuencia resultante es la convolución de la función de entrada p y la función del canal de comunicación v.
◦ La secuencia muestra la señal original más las réplicas retrasadas.
5. Compare el ccepstrum de la señal de salida con los cepstra de las secuencias originales. Vuelva a centrar los resultados para facilitar la comparación.
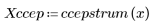
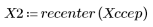
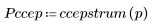
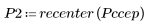
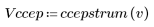
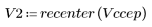
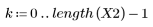
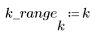
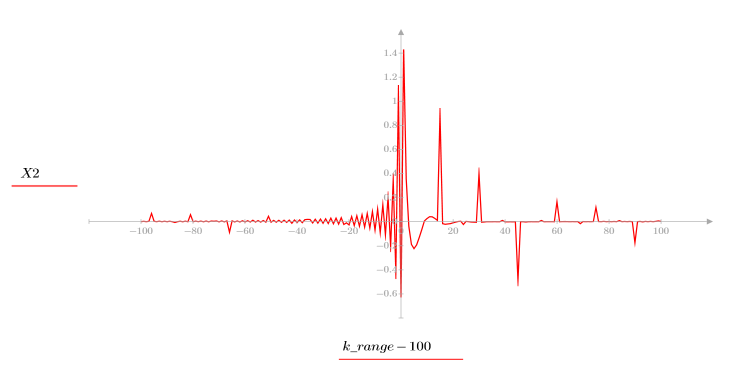
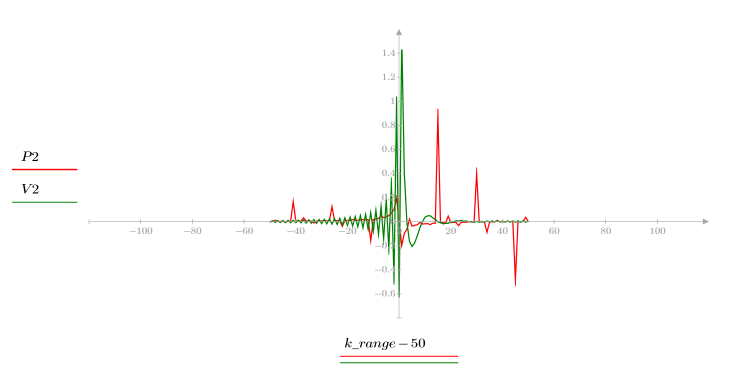
Los gráficos anteriores muestran que el ccepstrum de la señal de salida es la suma de los cepstra complejos de las dos secuencias que se combinaron.