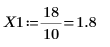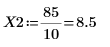Ejemplo: Funciones de Bessel de primera especie
Muestre la relación entre las funciones J0, J1 e Jn. Muestre también las relaciones entre estas funciones y sus versiones escaladas.
1. Defina dos variables de rango de paso:
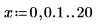
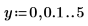
2. Trace las funciones J0 y J1. Añada la función de segundo orden Jn al gráfico:
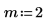
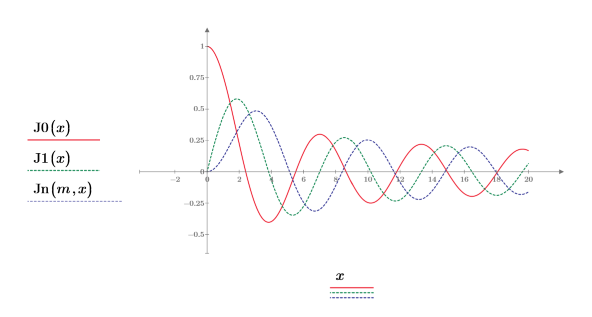
3. Cree un gráfico para mostrar que J0(y)=Jn(0,y). Redefina los valores de marca de graduación para ampliar el eje X con el fin de mostrar más detalles:
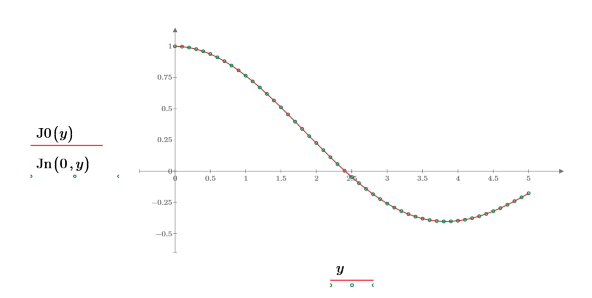
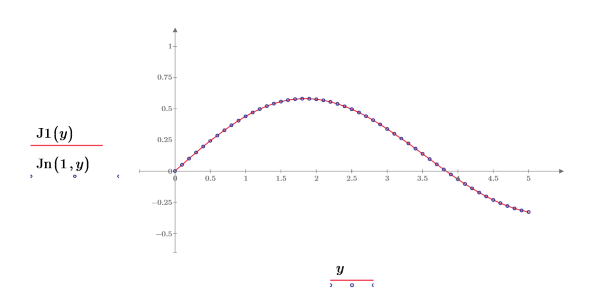
4. Cree un gráfico para mostrar que J1(y)=Jn(1,y). Redefina los valores de marca de graduación para ampliar el eje X con el fin de mostrar más detalles:
5. Utilice la evaluación simbólica para mostrar la relación entre cada función de Bessel de primera especie y su versión escalada:
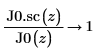
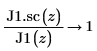
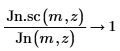
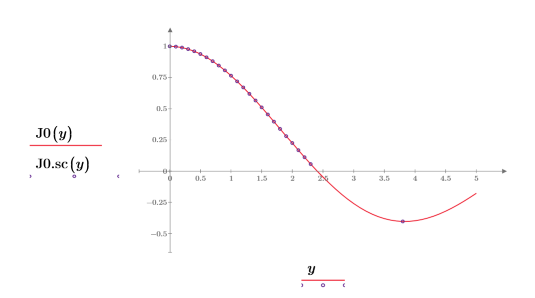
6. Cree un gráfico para mostrar que:
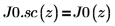
J0.sc contiene elementos complejos, por lo que debe aplicar primero la función Re para mostrar solo la parte real de los números.
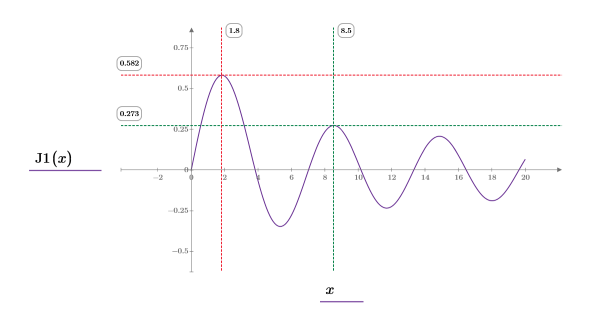
7. Calcule las coordenadas de los dos primeros picos de J1. Utilice las funciones augment y localmax para identificar los picos que están dentro del rango especificado:
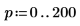
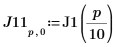
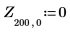
La función localmax requiere una matriz de entrada de dos columnas. La función augment se usa para crear esta matriz.
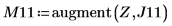
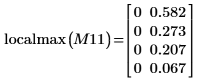
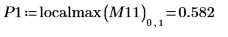
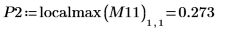
8. Utilice la función match para buscar las coordenadas horizontales de los picos. Reduce el valor de TOL para obtener los resultados más precisos:
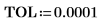
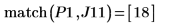
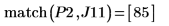
9. Añada marcadores al gráfico para marcar los dos primeros picos:
La variable del rango de paso presenta un paso de 0.1. Esto significa que los picos se producen en 1/10 del índice de elementos identificado por la función match o 1.8 y 8.5, respectivamente.