Ejemplo: funciones de Bessel
Use las funciones esféricas de Bessel y de Hankel para encontrar las soluciones a la ecuación de Schrödinger en el pozo cuadrado 3D (un átomo).
La solución representa las energías permitidas en las que las funciones de onda interna y externa tienen valores iguales y derivadas primeras. Estas energías existen para cada valor del momento angular (L).
1. Defina la masa, la constante de Plank y el radio del núcleo:
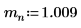
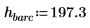
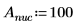
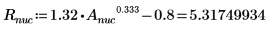
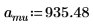
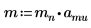
2. Defina el momento angular en cero:
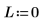
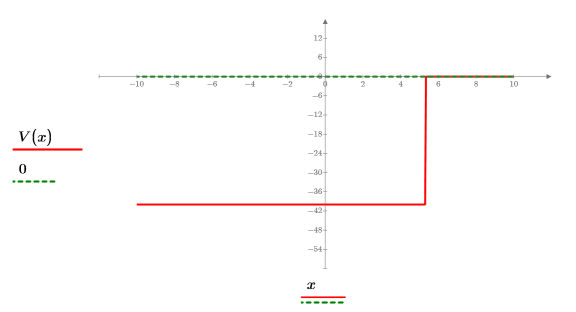
3. Defina y trace la energía potencial del pozo:
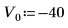
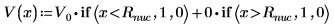
4. Utilice las funciones de Bessel esférica y de Hankel esférica para encontrar las soluciones:
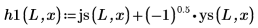
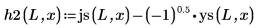
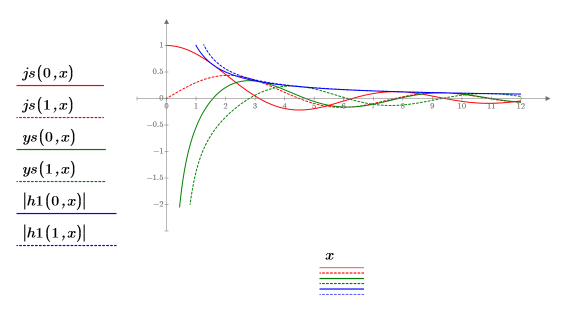
5. Defina, para los estados vinculados E < 0, las funciones de onda de la primera solución de estado de energía dentro y fuera del pozo:
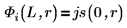
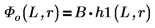
B es la normalización relativa.
6. Defina las constantes de propagación:
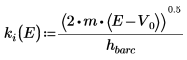
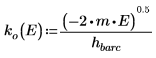
El argumento de la solución fuera del pozo es imaginario, porque la onda decrece fuera del pozo de potencial.
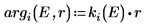
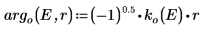
7. Asocie las funciones de onda en el borde del pozo (el radio del núcleo) para determinar la normalización relativa:
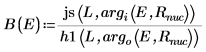
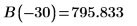
8. Asocie las derivadas. Determine autovalores mediante la búsqueda de coincidencias de las derivadas.
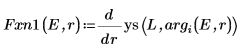
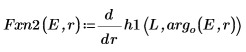
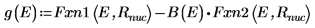
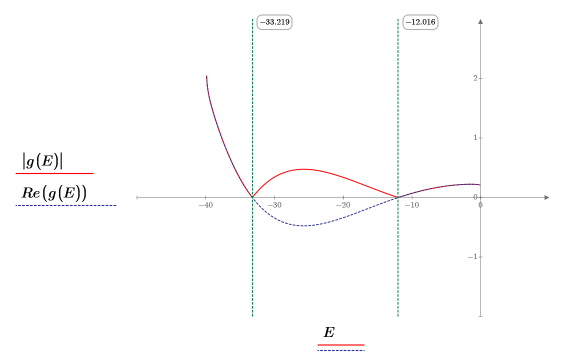
9. Proporcione dos valores de prueba para E:
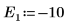
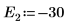
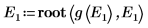
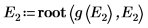
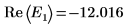
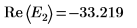
10. Trace g(E) frente a E y añada marcadores verticales para mostrar los dos puntos de la raíz: