Ejemplo: funciones de Airy
Muestre la relación entre las funciones Ai, Bi, DAi y DBi. Muestre también las relaciones entre estas funciones y sus versiones escaladas.
1. Utilice la evaluación simbólica para mostrar que la función DAi es la derivada primera de la función Ai, y que la función DBi es la derivada primera de la función Bi:
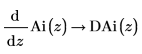
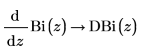
2. Defina una variable de rango de paso horizontal y, a continuación, trace las funciones Ai y Bi:
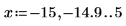
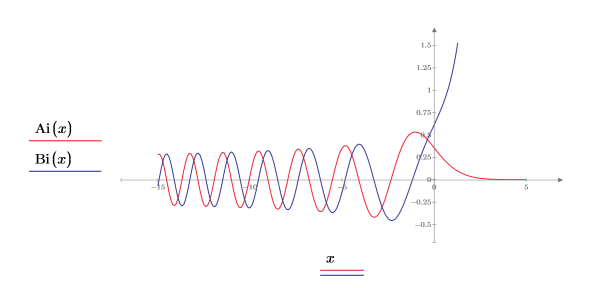
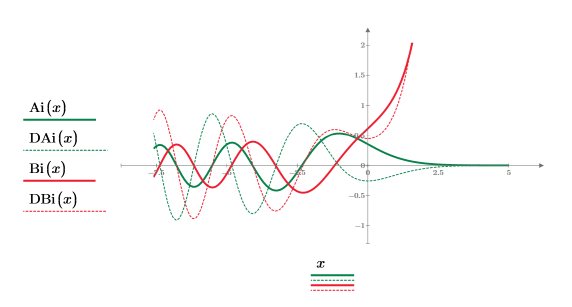
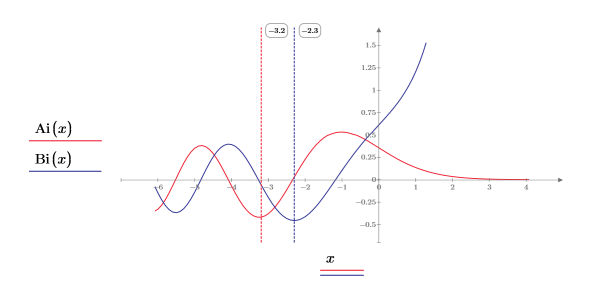
Las dos funciones tienen un aspecto similar, pero varían en la fase, a lo largo del eje X hasta que comienzan a discrepar a medida que -x se aproxima a cero.
3. Define los vectores Z1 y Z2 mediante Ai y Bi:
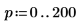
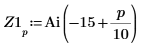
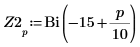
4. Utilice las funciones min y match para buscar las coordenadas coincidentes de los mínimos de Ai y Bi:
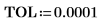
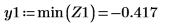
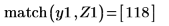
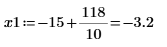
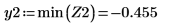
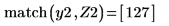
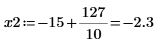
5. Añada marcadores verticales para mostrar los últimos mínimos antes de que las funciones comiencen a discrepar:
6. Utilice la evaluación simbólica para mostrar la relación entre cada función y su versión escalada:
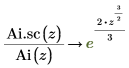
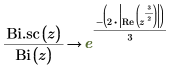
7. Cree un gráfico para mostrar que:

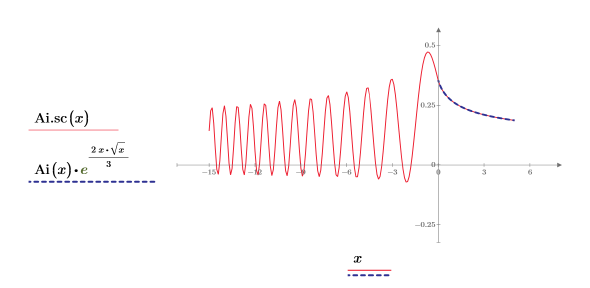
La segunda traza presenta valores complejos para los valores negativos de x.
8. Recree el gráfico anterior para mostrar los valores reales de la segunda traza:
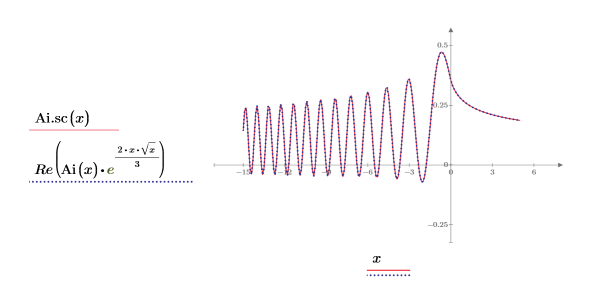
9. Trace las funciones DAi y DBi:
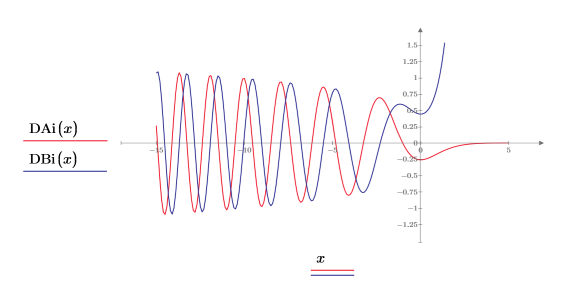
Las dos funciones tienen un aspecto similar, pero varían en la fase, a lo largo del eje X hasta que comienzan a discrepar a medida que -x se aproxima a cero.
10. Guarde DAi y DBi en los vectores Z11 y Z21 respectivamente:
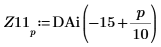
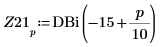
11. Busque las coordenadas de los mínimos locales de las funciones DAi y DBi más próximas a cero.
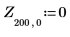
La función localmin requiere una matriz de entrada de dos columnas. El vector Z es utilizado por la función augment para crear una matriz de este tipo.
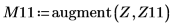
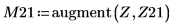

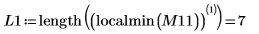
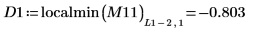

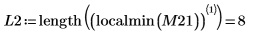
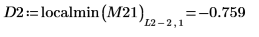
12. Busque las coordenadas coincidentes de los mínimos de DAi y DBi:
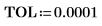
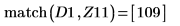
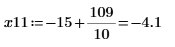
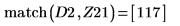
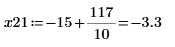
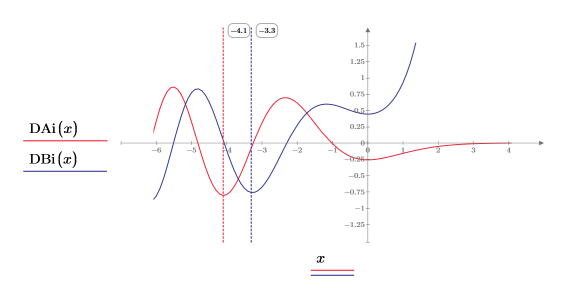
13. Añada marcadores verticales para mostrar los últimos mínimos antes de que las funciones comiencen a discrepar:
14. Utilice la evaluación simbólica para mostrar la relación entre cada función y su versión escalada:
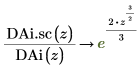
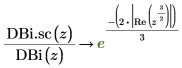
15. Cree un gráfico para mostrar que:
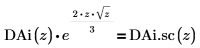
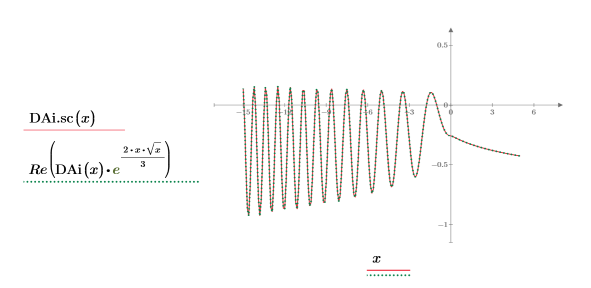
16. Compare las funciones Ai, DAi, Bi y DBi trazándolas en el mismo gráfico: