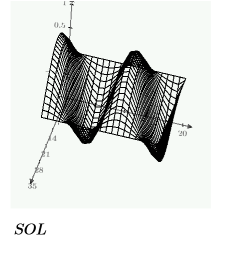
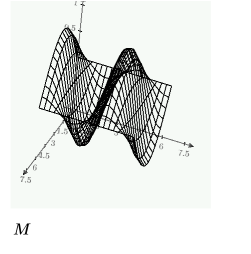
Ejemplo: PDE en bloques de resolución
Utilice una ecuación diferencial parcial (PDE) en el bloque de resolución y el solver de ecuación diferencial parcial numol para comparar las soluciones de una ecuación de onda.
Bloque de resolución de PDE
Para resolver la siguiente ecuación de onda unidimensional:
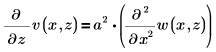
Utilice la restricción:
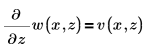
Para proyectar la primera ecuación como un sistema de dos ecuaciones diferenciales parciales, defina un bloque de resolución de PDE.
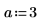
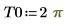
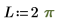
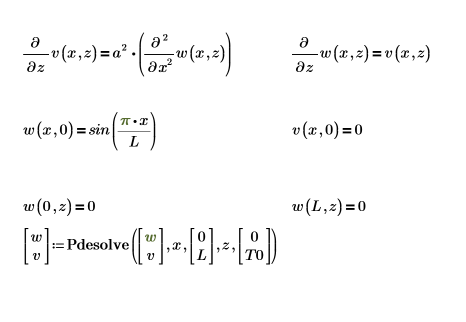
A continuación, se indica una solución única en el límite:
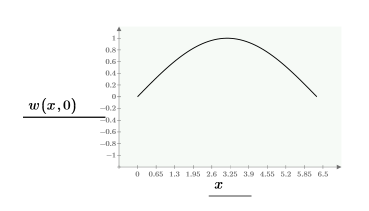
Cree una cuadrícula de soluciones que se trazarán tridimensionalmente con la función CreateMesh utilizando las restricciones definidas anteriormente:
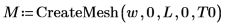
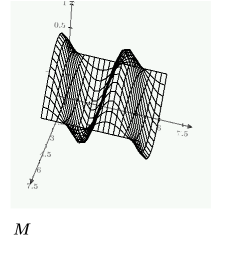
Uso de numol
Puede resolver el solver de la línea de comandos numol. Esto resulta especialmente útil cuando desea incluir el cálculo en un programa.
Defina el número de ecuaciones diferenciales parciales y restricciones algebraicas en el sistema:
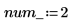
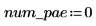
La función para evaluar el lado derecho de las PDE es un vector de longitud num_pde + num_pae (ecuaciones algebraicas parciales). En este caso, la función es un sistema de ecuaciones. De forma similar, la condición de límite se define como un vector de columna de longitud num_pde + num_pae.
La expresión del vector de PDE:
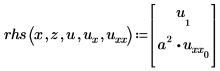
Por tanto, u1=v, tal como se ha definido anteriormente, y u0=w.
El vector de las condiciones iniciales:
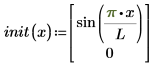
Supongamos que cada lado izquierdo es la derivada de tiempo de primer orden del vector de función desconocido u. Las variables de la función son x (espacio) y t (tiempo). La solución es u, que también puede ser un vector de soluciones para un sistema de ecuaciones: ux, la primera derivada de cada solución u en el vector, y uxx, la segunda derivada espacial.
Debe utilizar subíndices vectoriales para dirigir las entradas individuales en u, ux y uxx.
El vector de condiciones de límite puede tener tres tipos de filas. Cada fila viene determinada por una de las siguientes opciones:
• rhs contiene derivadas espaciales de segundo orden: se requieren dos condiciones de límite ("D" de Dirichlet o "N" de Neumann), una para cada lado de la región de integración.
• rhs contiene derivadas espaciales de primer orden: una condición de límite de Dirichlet en el lado izquierdo o derecho de la región de integración. La otra es "NA".
• Si el vector no contiene derivadas espaciales, no se requiere ninguna condición de límite.
Las condiciones de límite de los bordes izquierdo y derecho siguen estas convenciones:
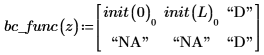
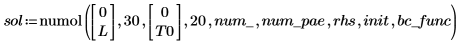
El resultado de numol es una matriz que representa cada punto en el espacio como una fila y cada punto en el tiempo como una columna. Esto facilita la visualización de las soluciones, ya que le permite seleccionar una columna a la vez y representar la solución en todo el espacio en un único punto del tiempo. Al resolver un sistema de ecuaciones, la matriz de la solución de cada función desconocida se incorpora al lado de la matriz anterior.
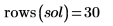
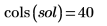
En el ejemplo actual, cada función tiene 20 puntos en el tiempo, por lo que la matriz incluye 40 columnas. Seleccione la primera solución: u0
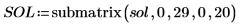
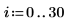
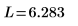
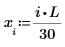
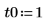
Comparación entre numol y Pdesolve
Compare las soluciones de numol y Pdesolve en un punto t0:
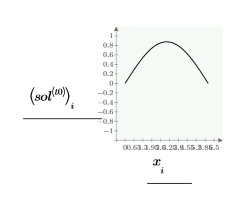
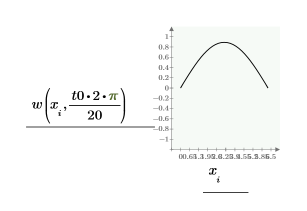
Compare la cuadrícula de soluciones para los valores de espacio y tiempo: