Funciones integrales elípticas
Las funciones integrales elípticas son un grupo de funciones integrales de la siguiente forma:
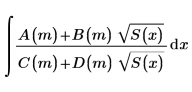
A(m), B(m), C(m) y D(m) son polinomios, y S(x) es un polinomio de grado 3 o 4. Las funciones integrales elípticas son útiles en muchos problemas computacionales, entre los que se incluyen el electromagnetismo y la gravitación.
Puede utilizar funciones integrales elípticas de forma completa o incompleta. La forma completa calcula la integral de 0 a 1. La forma incompleta calcula la integral de 0 a una variable z. En Mathcad, puede utilizar las siguientes funciones integrales elípticas:
• ellipticK: integral elíptica completa de primera especie:
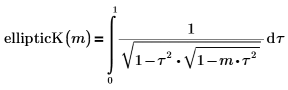
• ellipticF: integral elíptica incompleta de primera especie:
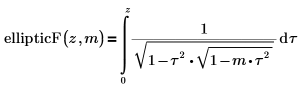
• ellipticE: integral elíptica completa de segunda especie:
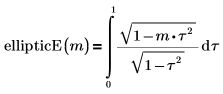
• ellipticE: integral elíptica incompleta de segunda especie:
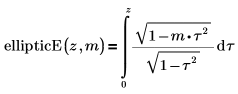
• ellipticPi: integral elíptica completa de tercera especie:
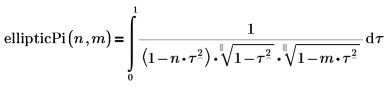
• ellipticPi: integral elíptica incompleta de tercera especie:
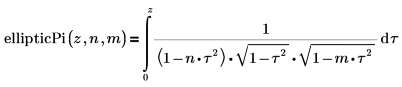
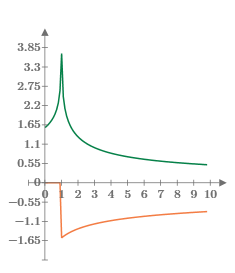
Consulte el comportamiento de la función ellipticK comprendida entre 0 y 10. El resultado es un número real cuando 0<m<1 y un número complejo si m>1.
La curva verde representa los resultados reales, y la curva naranja, los resultados complejos.
Argumentos
• m es un escalar o un vector.
• n y z son escalares.