Derivación de condiciones iniciales de EDO
Las siguientes funciones se utilizan con problemas de valor de límite en los que no se conocen todas las condiciones iniciales.
• bvalfit(v1, v2, x1, x2, xf, D, load1, load2, scoreb)
• sbval(v1, x1, x2, D, load1, scorei)
Permite devolver un vector que contiene los valores iniciales que están sin especificar en x1 para EDO o sistemas de EDO identificados en D. Estos valores iniciales se pueden utilizar en uno de los solvers de EDO. Si conoce algunos valores de la solución y las n − 1 primeras derivadas en un valor intermedio, utilice bvalfit. Esto es muy útil cuando la derivada presenta una discontinuidad en algún punto del intervalo de integración. Si conoce algunos valores en los puntos iniciales y finales, utilice sbval. El problema de valor de límite se convierte en un problema de valor inicial por disparo desde los extremos y uniendo las trayectorias de la solución y sus derivadas en un punto intermedio.
Argumentos
• v1 y v2 son vectores de aproximaciones reales de los valores iniciales que están sin especificar en x1.
• x1 y x2 son los extremos reales del intervalo en el que se evalúa la solución de las ecuaciones diferenciales.
• xf es un punto intermedio real entre x1 y x2 en el que las trayectorias de las soluciones se restringen para ser iguales.
• D(x, y) es una función de n elementos con valores vectoriales de la variable independiente (x) y un vector de funciones (y) que contiene las ecuaciones de las derivadas primeras de todas las funciones desconocidas en el sistema de EDO.
Para crear este vector, formule las ecuaciones con un término de derivada primera en la izquierda, sin multiplicadores y sin derivadas de orden superior en la ecuación. Por ejemplo, un EDO simple de la función y(x) que contiene una derivada segunda debe escribirse como un sistema de ecuaciones en y0(x) y y1(x), donde la derivada primera de y0 es y1. El EDO siguiente de una sola función se reescribe para el solver con subíndices de vector:
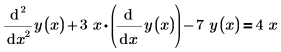
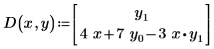 | con lado izquierdo implícito | 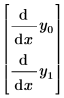 |
• load1(x1, v1), load2(x2, v2) son funciones reales con valores vectoriales cuyos elementos corresponden a los valores de yn en x1 y x2, respectivamente. Algunos de estos valores son condiciones iniciales conocidas. Los valores desconocidos se definen como los valores de prueba correspondientes de v1 y v2, respectivamente.
• scoreb(xf, y) es una función real con valores vectoriales utilizada para especificar cómo deben coincidir las soluciones en xf. En general, tiene que definir scoreb(xf, y):= y para hacer que las soluciones de todas las funciones desconocidas coincidan en xf.
• scorei(x2, y) es una función real con valores vectoriales que tiene el mismo número de elementos que v. Cada elemento es la diferencia entre una condición inicial en x2, tal como se especificó originalmente, y el cálculo aproximado correspondiente del solver. El vector score mide el grado en que una solución propuesta coincide con las condiciones iniciales en x2. Un valor de 0 para cualquier elemento indica una coincidencia perfecta.