Rules for Functions numer and denom
• Any expression is equivalent to itself divided by 1 and therefore, for expressions that do not contain division, numer will return the expression and denom will return 1.
|
Numerator
|
Denominator
|
|---|---|
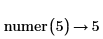 |
 |
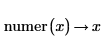 |
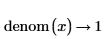 |
 |
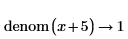 |
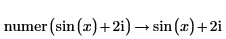 |
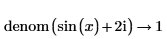 |
• Fractions are not simplified before taking numerator and denominator.
|
Numerator
|
Denominator
|
||
|---|---|---|---|
 |
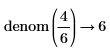 |
||
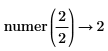 |
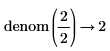 |
||
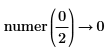 |
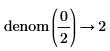 |
||
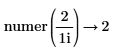 |
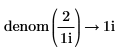 |
||
|
|||
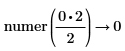 |
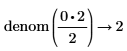 |
||
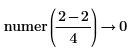 |
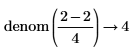 |
||
• For more than one fraction, the least common multiple of denominators and corresponding sum of the numerators are calculated. No further simplification is done.
|
Numerator
|
Denominator
|
Evaluation
|
|---|---|---|
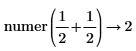 |
 |
|
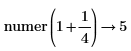 |
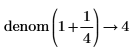 |
|
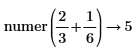 |
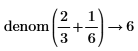 |
|
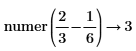 |
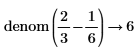 |
|
 |
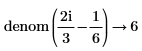 |
 |
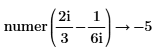 |
 |
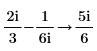 |
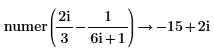 |
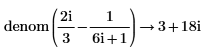 |
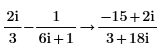 |
 |
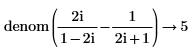 |
 |
• When the sum of fractions is present in the numerator or denominator, results are returned as-is, without fractions reductions.
|
Numerator
|
Denominator
|
Evaluation
|
||
|---|---|---|---|---|
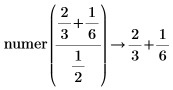 |
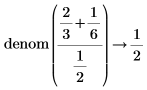 |
|||
 |
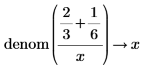 |
|||
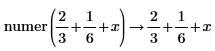 |
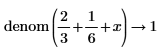 |
|||
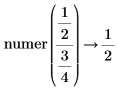 |
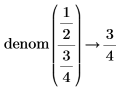 |
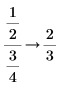 |
||
 |
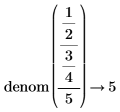 |
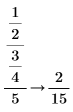 |
||
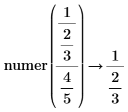 |
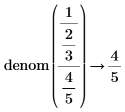 |
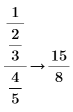 |
||
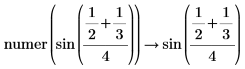 |
 |
|||
|
||||
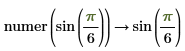 |
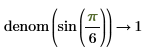 |
 |
||
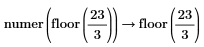 |
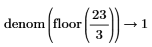 |
 |
||
• For explicit fractions, the numerator and denominator are taken as-is without reduction.
|
Numerator
|
Denominator
|
|---|---|
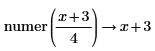 |
 |
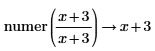 |
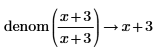 |
 |
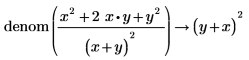 |
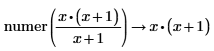 |
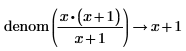 |
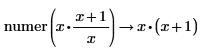 |
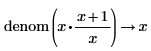 |
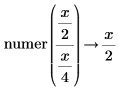 |
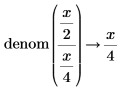 |
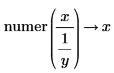 |
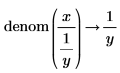 |
• General expressions of integers are returned in explicit form without reduction in division.
|
Numerator
|
Denominator
|
|---|---|
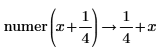 |
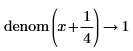 |
 |
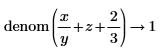 |
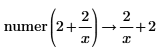 |
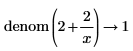 |
 |
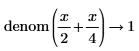 |
 |
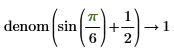 |
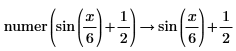 |
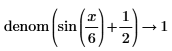 |
• For expressions with calculus operators (derivative, integral, limit, range product, and range summation) calculation is performed and then above rules are followed.
|
Numerator
|
Denominator
|
|---|---|
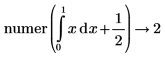 |
 |
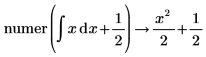 |
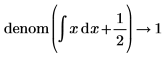 |
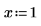 |
|
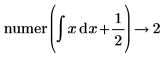 |
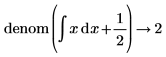 |
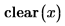 |
|
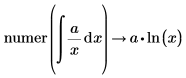 |
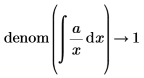 |
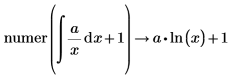 |
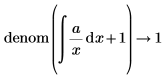 |
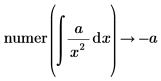 |
 |
 |
 |
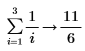 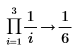 |
|
 |
 |
• For expressions with floating-point or complex floating—point numbers, division is performed, and the result is returned as numer. For expressions with floating or complex floating with variables, division is not performed, and the result is returned as a general expression of a complex integer.
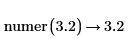 |
 |
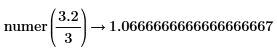 |
 |
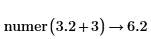 |
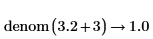 |
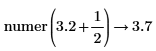 |
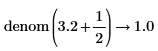 |
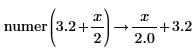 |
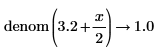 |
 |
 |
 Division of numbers is performed here. |
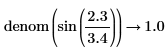 |
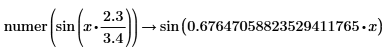 Division of variables is preserved here. |
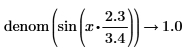 |
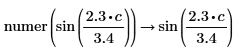 |
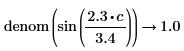 |
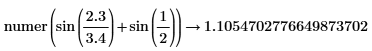 |
 |
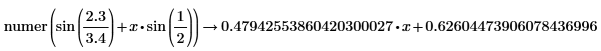 |
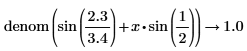 |