Non-Convergence of Numerical Evaluation of Integrals with Infinite Limits
This topic provides a workaround for two cases of non-convergence errors when numerically evaluating integrals with one or two infinite integration limits.
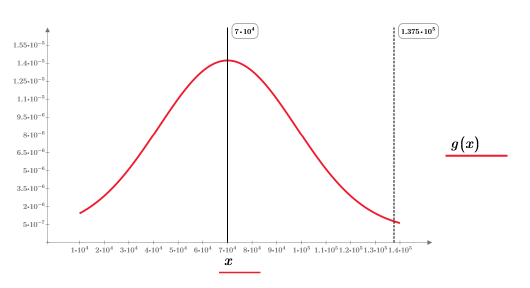
To explain the two cases, define a mean μ and a standard deviation σ.
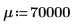
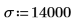
Case I: Integral with One Infinite Integration Limit
Set multiplier variable n to 1, and then define function g(x) in terms of the built-in probability density function dnorm.
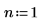
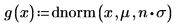
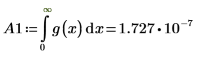
When n=1, evaluating the integral of g(x) over the range [0, ∞] does not return an error, but returns a very small value.
Workaround for Case I
Increase the value of n to n=2 and re-evaluate the integral.
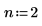
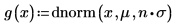
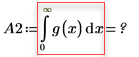
Increasing the value of n to n=2 results in an error because the calculation is not converging to a solution.
As a workaround, set variable T to a value that is close to the tail of g(x), and then split the single integral into two: one that covers range [0, T] and one that covers range [T, ∞].
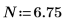 | 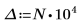 |
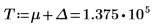 |
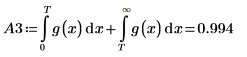
The split integral A3 returns a good answer when n=1 or n=2. Plot g(x) and add vertical marker T to see how close it is to the tail of g(x).
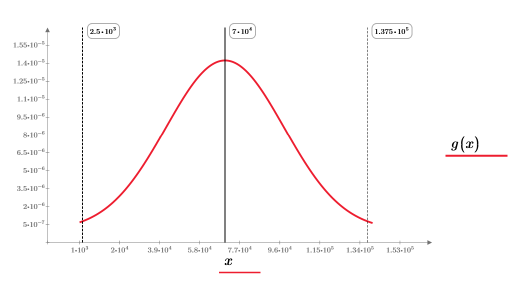
The plot shows variable T as the vertical marker close to the tail of g(x).
Case II: Integral with Two Infinite Integration Limits
Set the multiplier variable n to 1, and then evaluate the integral of g(x) over the range [-∞, ∞].
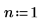
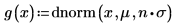
When n=1, evaluating the integral of g(x) over the range [-∞, ∞] returns no error but the returns a very small value.
Workaround for Case II
As a workaround, set variables T1 & T2 to values that are close to the head and tail of g(x), and then split the single integral into three integrals: one to cover range [-∞, T1], one that covers range [T1, T2], and one that covers range [T2, ∞].
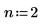
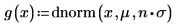
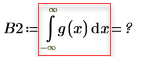
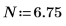 | 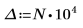 |
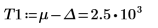 | 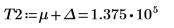 |
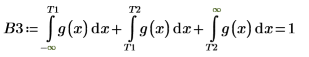
The split integral returns a good answer when n=1 or n=2. Plot g(x) and add vertical markers T1 and T2 to see how close they are to the head and tail of g(x).
Observations and Conclusions
Plot the built-in probability density function dnorm using the same mean but two different values of standard deviation.
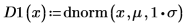
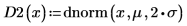
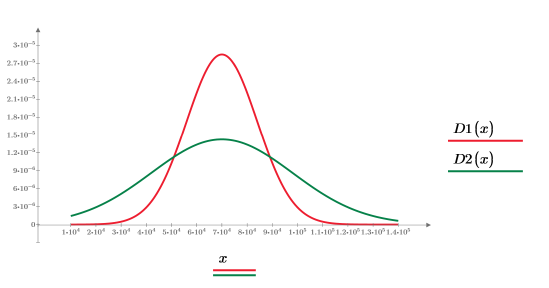
The plot shows that:
• the smaller standard deviation value causes the bulk of the area under the curve to be closer to the mean. In this case, the numerical calculation converges but returns the wrong answer.
• the larger standard deviation value causes the bulk of the area under the curve to be spread away from the mean. In this case, the numerical calculation fails to converge.
In both cases, splitting the integral ensures that the calculation converges and returns the correct answer.