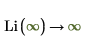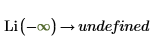Example: Logarithmic Integral Functions
Logarithmic Integral Functions
1. Evaluate li function when x=2.4.
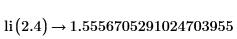
2. Evaluate li function when x=2:
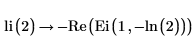
The evaluation returns an expression.
To receive numeric results, you can use decimal digits:
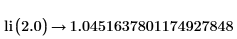
3. Another option for receiving numeric results is to use the float keyword. Evaluate li function when x=ⅇ:
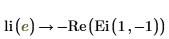
And using the float keyword:
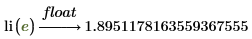
4. li has a single positive zero. Use the assume keyword to solve for positive values of x.
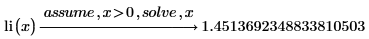
5. Use the limit operator and symbolically evaluate logarithmic integral functions as its argument approaches infinity:
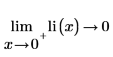
The limits on both sides of branch cut are different:
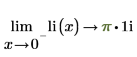
6. The logarithmic integral function has one singularity point on x=1.
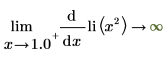
Offset Logarithmic Integral Functions
1. Evaluate the offset logarithmic integral function Li when x=2.4:
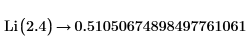
2. Evaluate Li when x=ⅇ.
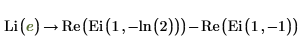
You can see that, similarly to li function, the evaluation returns an expression. To receive numeric results, use the float keyword:
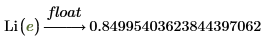
3. Evaluate Li when x=∞ and x=-∞: