Example: T-Test on Normal Means
Test the hypothesis that two normal populations have equal means.
1. Define data sets to compare.


2. Collect the sample statistics.
Number of samples for each data set | 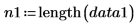 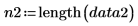 | 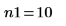 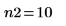 |
Sample means | 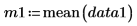 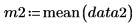 | 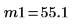 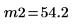 |
Sample standard deviations | 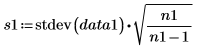 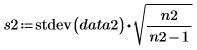 | 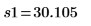 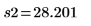 |
Degrees of freedom when combining the two means | 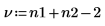 | 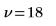 |
Standard error of the difference in the data sets | 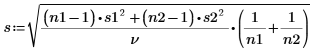 | 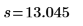 |
3. Define the significance level.
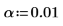
4. Calculate the test statistic.
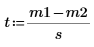
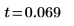
5. State the null and the alternative hypothesis.
H0: m1 ≤ m2
H1: m1 > m2
6. Calculate the p-value and test the hypothesis. In this example, all of the Boolean expressions evaluate to 1 when the null hypothesis is true (you do not reject H0).
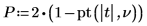
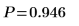
There is a 0.946 probability that the test statistic is greater than the one observed, assuming that the null hypothesis is true. The comparison between the p-value and the significance level indicates there is no evidence that the alternative hypothesis is true.
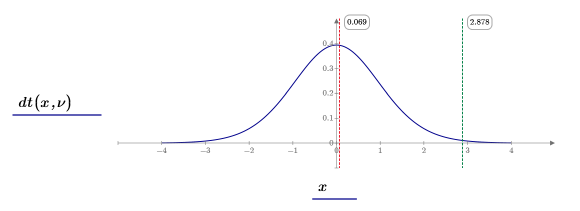
7. Calculate the limit of the critical region and test the hypothesis.
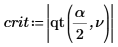
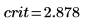
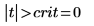
Accept the null hypothesis. There is no evidence that the m1 is greater than m2.
8. Plot the student distribution (blue), the boundary of the critical region (green), and the test statistics (red).