Example: The Short-Time Fourier Transform
Use the stft function to calculate the short-time Fourier transform (STFT) of a signal whose spectral characteristics change over time.
The function returns a matrix whose columns contain the Fourier transform of the input signal at times separated by s samples. For a signal x(t), the STFT is defined in continuous time as:
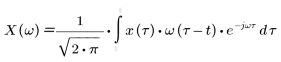
where w(t) is a sliding real-valued window taper used to localize the influence of the transform around a specific time.
Two-Pitch Signal
The following signal is composed of two sinusoids of different frequencies occurring at different times.
1. Define the signal components.
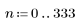
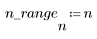
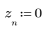
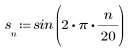
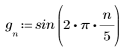
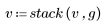
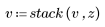
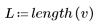
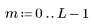
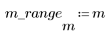
2. Plot the composite signal.

The STFT contains information on the frequency content of the signal and the time at which the frequency is present.
3. Calculate the STFT with 100 frequency samples, a time step of 30 and a Hanning window.
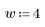
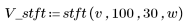
This is a 100 x 56 matrix (there are 56 time-steps of 30 in the signal of length L)
4. Calculate the squared magnitude.
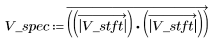
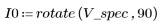
5. Save the resulting contour as a BMP image.
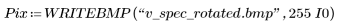

(v_spec_rotated.bmp)
The image shows not only the two frequencies, but also the time at which they occur. However, the spectrogram suffers from what is called the localization trade-off. To achieve time localization (that is, the STFT pinpointing the times at which the sinusoids are active), requires a short window in the time domain. Conversely, good frequency localization requires a long time window. This trade-off is further dependent on the type of window used, the signal under consideration, time, and frequency.
6. To illustrate, calculate the STFT and the spectrogram of the same signal as above, but using a frequency window length of 300 instead of 100.
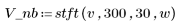
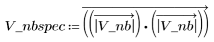
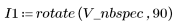
7. Save the resulting contour as a BMP image.
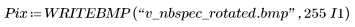

(v_nbspec_rotated.bmp)
The STFT calculated with a long window has a better frequency resolution, but its time resolution is not as good. This time-frequency trade-off can be avoided by using other time-frequency functions; such as timefreq and timecorr.
Custom Windowing
The frequency window in this example is zero-padded up to the length of the Fourier transform.
1. Define the window length and the percentage of raised cosine.
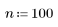
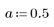
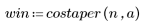
The length of the window cannot be longer than the length of the Fourier transform.
2. Rescale the window coefficients so that the window has unit energy.
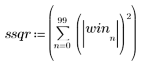
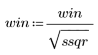
3. Calculate the STFT and the spectrogram.
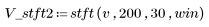
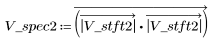
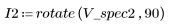
4. Save the resulting contour as a BMP image.
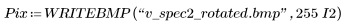

(v_spec2_rotated.bmp)
Try changing the parameters of the stft function, or the frequencies of the sinusoids in the input signal and observe how the plots change.