Example: Symbolic Solutions of Equations
Solve equations symbolically in one or many unknowns.
Solving a Single Equation
1. Type the following equation:
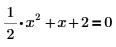
2. Insert the symbolic evaluation operator, type the keyword solve in the placeholder, and press Enter.
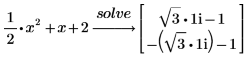
Since the right side of the equation is 0, you do not need to type the =0 part of the expression. |
3. Type the constant 2 in decimal format as 2.0 to return the answer in floating-point format.
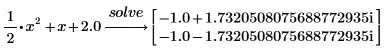
4. Solve an equation with one variable.
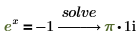
5. Solve an equation with multiple variables.
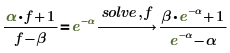
When the equation contains multiple variables then you must specify the variable to solve for. |
6. Solve a fourth-order polynomial.

The above result shows that the symbolic solution of a fourth-order polynomial yields four numeric solutions. |
7. Find the roots of a polynomial with parameterized coefficients.
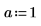
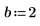
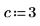
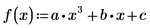
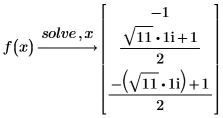
Solving Systems of Equations and Equalities
You can solve several equations and equalities together as a system of equation by grouping them in a vector.
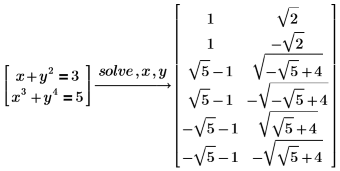
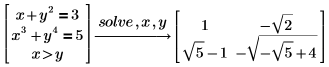
Solving Polynomials in Radicals
By default, PTC Mathcad solves polynomial equations up to degree 4 in radicals. The solutions are built up, using the ordinary operations of arithmetic, in terms of radicals.
1. Solve the following polynomial:
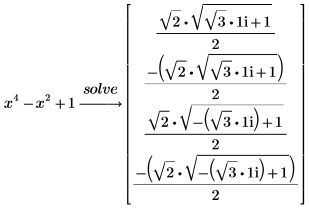
Mathematician Galois proved in the nineteenth century that there are polynomials of degree 5 and greater that cannot be solved in radicals. For these polynomials, PTC Mathcad returns a numerical approximation for the roots. |
2. Solve a polynomial of degree 5.

The above result shows that the symbolic solution of a fifth-order polynomial yields five numeric solutions. |
Making Assumptions About the Domain of a Variable
Use the keyword assume to make assumptions about the domain of a variable in the problem, for example, that it is a real number.
1. Solve an equation assuming that x is a real number.
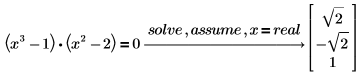
PTC Mathcad returns only the real solutions to the equation. |
2. Use RealRange to find the real solutions in the range (0, 2).
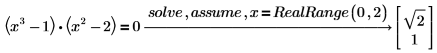
3. Type x=integer to find just the integer solutions.
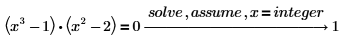
4. Use assume to restrict the domain of a variable in a symbolic evaluation.
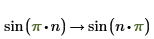
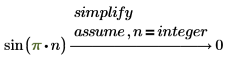
Returning Detailed Solutions to Equations
Add the modifier fully after solve to return detailed solutions to equations.
1. Use function clear.sym to clear the previous symbolic value of a.
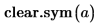
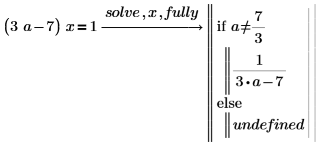
2. Use fully to return the values of a for which the solution is valid.
3. Use the detailed result to define a function.
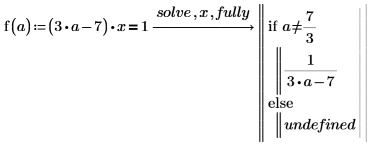
4. Evaluate the function at a=3 and a=7/3:
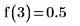
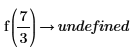
Equations with Periodic Solutions
For equations whose solution is periodic, PTC Mathcad returns a single solution, followed by an expression for adding integer multiples of the period to the first solution.
1. Use fully to evaluate sin(x).
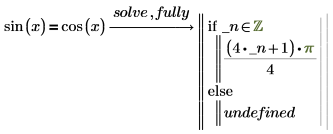
The expression following the if statement means pi/4 plus all integer multiples of pi. PTC Mathcad inserts a new generated variable _n that represents an arbitrary integer. An underscore is inserted before the generated variable to avoid name conflicts with other variables that might be defined elsewhere in the worksheet. |
2. Add the modifier using, followed by an equation written using Boolean equal to operator to set the generated variable equal to the new variable.
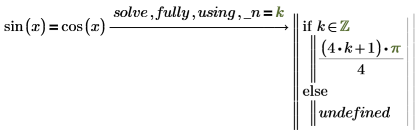
If the variable you specify after using is not the generated variable that solve would have returned, PTC Mathcad returns an error.