Example: Seeded Iteration and Difference Equations
Estimate solutions using seeded iteration.
Square Roots
Use the Babylonian method to approximate the square root of a number.
1. Define a positive real number X and a guess value of its square root.
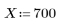
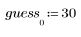
The first guess is defined as the first element of a vector.
2. Define N to be the number of iterations.
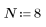
3. Calculate new estimates of the square root.
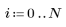
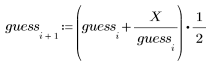
 | 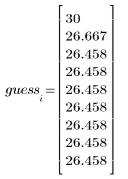 | 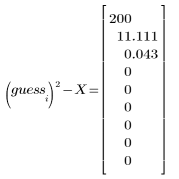 |
The built-in square root function gives the following result:
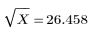
4. Plot the vector of estimates.
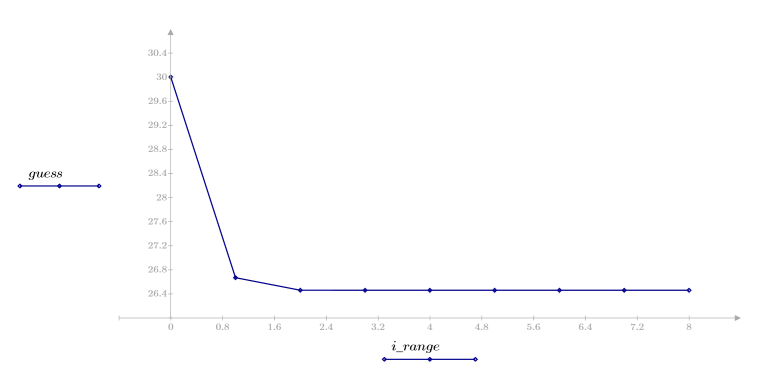
Here, convergence occurs very quickly. For other cases, you can increase the number of iterations N to suit the needs of the problem.
Systems of Difference Equations
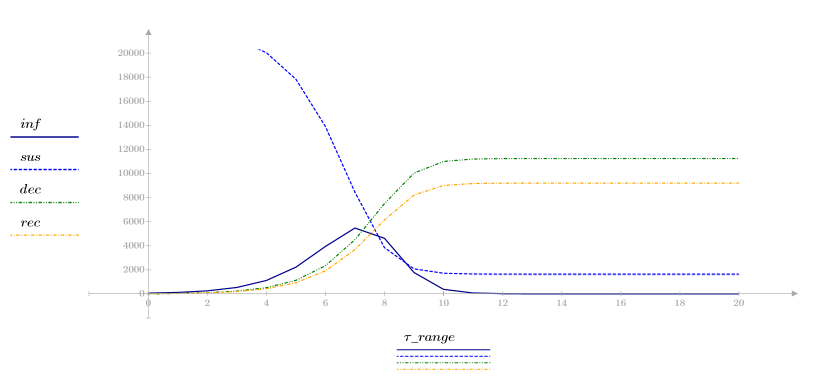
Consider an infection model with four variables:
• inf—The number of individuals infected
• sus—The number susceptible
• dec—The number deceased
• rec—The number recovered
1. Define seed values for the simultaneous iteration.

2. Define the system of difference equations.
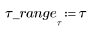
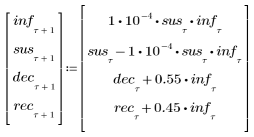
3. Plot the four variables against time to view how the infection model evolves.
Matrix Difference Equations
Consider a Markov process, that is, a vector time series whose present state is found by multiplying the previous state by a state transition matrix.
1. Define the initial vector state and the state transition matrix A.
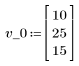

2. Define the iteration process.
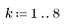
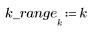
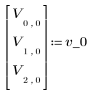
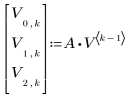
3. Calculate the final state of the vector.
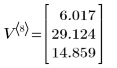
The matrix V contains the history of the process:
