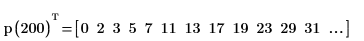Example: Recursive Functions
Use the PTC Mathcad programming abilities to define recursive functions.
Example 1: Defining the Factorial Function
1. Define function Fac that calculates the factorial of n. Label your function using the Function label.
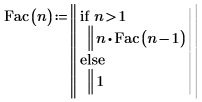
2. Calculate the factorial of 6 using Fac and check it using the PTC Mathcad factorial operator.
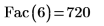
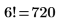
3. Define another function Fac with a different condition on n and call the function, as shown below.
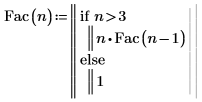
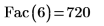
PTC Mathcad produces the same result because it is looking back at the previous definition of Fac to perform the calculation.
4. Disable the first definition of Fac to see the difference in the results. Avoid this ambiguity by not reusing function names.
Example 2: Computing the Greatest Common Divisor (GCD) of Two Positive Integers
1. Write a recursive function GCD that calculates the greatest common divisor of two numbers, which is the largest integer that evenly divides x and y.
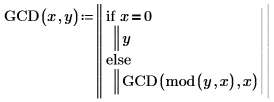
2. Call this function with various values.
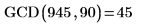 | 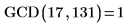 |
This program is the same as built-in greatest common divisor function gcd:
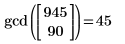 |  |
Example 3: Defining the nth Iterate of a Function f(x) at Point a
1. Write a recursive function nest that calculates the nth iteration of a function f(x) at point a.
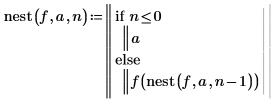
2. Define a function f(x) and assign 1 to a.
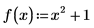
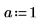
3. Call this function with various values.
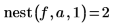 | 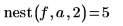 |
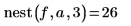 | 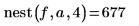 |
Example 4: Defining the Fibonacci Sequence (Two Recursive Calls per Invocation)
1. Write a function fib that calculates the value of Fibonacci sequence for n.
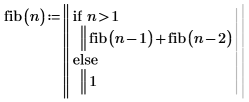
2. Define a vector k and call the fib function.
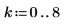

Example 5: Defining the Partition Function
1. Write a recursive function part that calculates the number of different ways to express m as a sum of positive integers not exceeding n.

2. Call the function with various values.
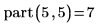
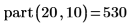
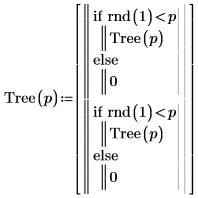
Example 6: Creating a Random Binary Tree
1. Write a recursive function Tree that creates a random binary tree.
2. Call the function.

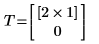
Example 7: Finding the Height of a Binary Tree
1. Write a recursive function height that returns the height of a binary tree.
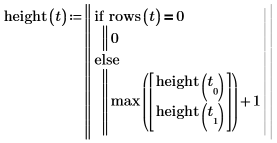
2. Call the function with the tree you created in the previous example.
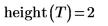
Since Tree creates a random binary tree, the returned height changes after each recalculation. |
Example 8: Setting Up the Sieve of Eratosthenes to Find Prime Numbers
1. Use the ceil function to write a recursive function p that calculates all prime numbers smaller than n, using the sieve of Eratosthenes.

2. Call the function to get a vector of all prime numbers smaller than 200.