Example: Rational Function Regression 2
rationalfitnp - No Poles
Use the rationalfit and rationalfitnp functions to perform rational function regression. When you use the rationalfitnp function instead of the rationalfit function, the solution to the traditional least-squares problem is checked for roots of the denominator within the fitting interval. If there are no poles, the generated fit is returned. If there are poles, additional constraints are added to the nonlinear optimization problem.
1. Define a data set by modifying slightly the inverse function of x.
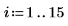
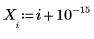
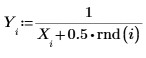
2. Specify an order for the numerator and denominator of the rational function.
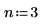
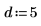
The fitting function has the following form:
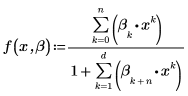
3. Define a confidence limit and a vector of standard deviations.
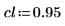
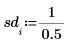
4. Call the rationalfit and the rationalfitnp functions.
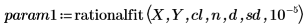 | 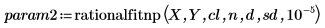 |
 |  |
For param1 and param2, the first column contains the parameters and the remaining columns contain the lower and the upper boundaries for each parameter at the confidence limit defined above.
5. Plot the data set and the two regression curves.
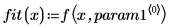
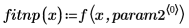
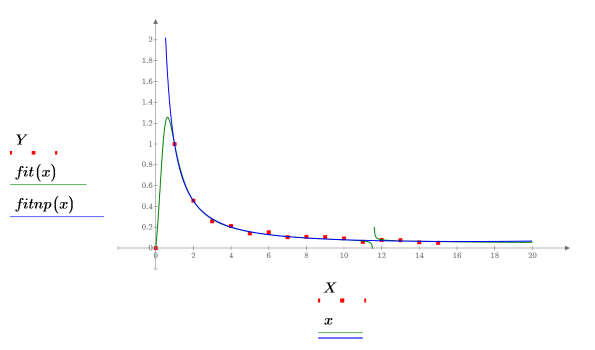
The pole was removed by the rationalfitnp function. Its denominator polynomial is cast in the following form:
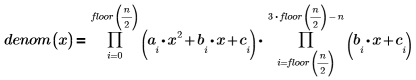
To avoid the pole, the following constraints were added:
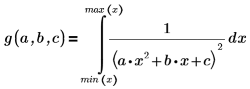
 |  |
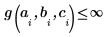 | 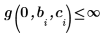 |
LeastSquaresFit
Compare the fitting curves returned by rationalfitnp and by LeastSquaresFit. The LeastSquaresFit function performs the same algorithm as the one for rationalfitnp, but it requires guess values and confidence limits for the parameters. You may wish to do this when you want the constant term to be in the numerator rather than in the denominator.
1. Define the fitting function.
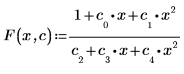
2. Define guess values for the parameters.
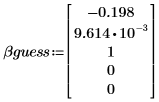
3. Define lower and upper boundary conditions for the parameters.

4. Call the LeastSquaresFit function.
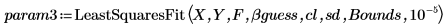
5. Plot the data set, and the fitting curves returned by the rationalfitnp, and the LeastSquaresFit functions.
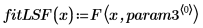
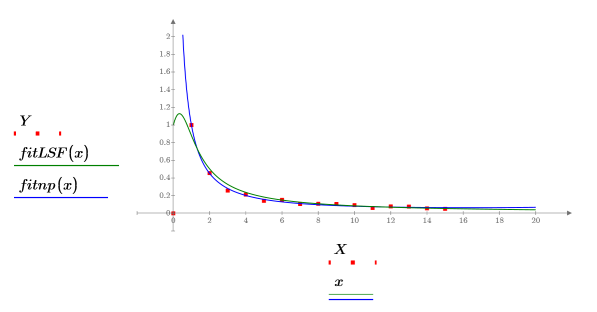
Any filtering or data transformation method that biases the data towards a straight line before doing a rational function fit will add considerable convergence speed to the rational function and may have a side benefit of getting rid of unwanted poles. |