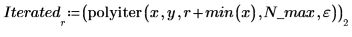Example: Polynomial Interpolation
polyint
Use the polyint function to perform polynomial interpolation on a data set.
1. Define a data set.


2. Call the polyint function to calculate the polynomial interpolation of the data set at a particular point.
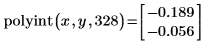
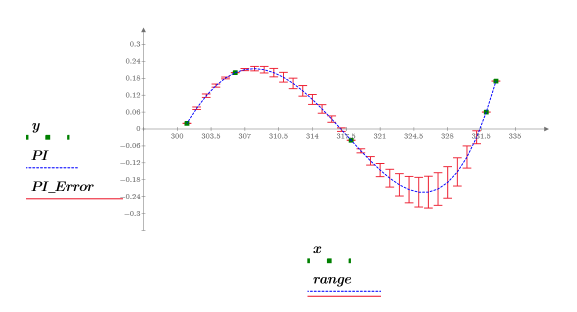
At x = 328, the interpolated result is y = -0.189, with an error of 0.056.
3. Define the range of x values where you want to find the interpolated y values.
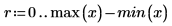
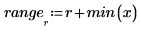
4. Record the interpolated values and their respective error.
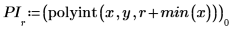
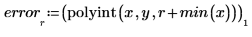
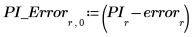
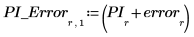
5. Plot the data points, the interpolated curve, and the error estimate.
polycoeff
To calculate the interpolated values, use polyint. To calculate both the interpolating polynomial and some of its derivatives, use polycoeff. The coefficients provided by polycoeff are less accurate at given data points, so they are not the best representation of interpolated values.
1. Find the polynomial coefficients for the polynomial curve that passes through the set of data points defined above.
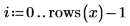
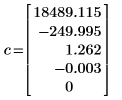
2. Define a polynomial function, where c is the vector of polynomial coefficients.
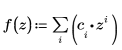
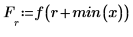
3. Differentiate the polynomial function.
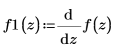
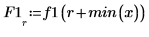
4. Plot the data points, the polynomial interpolation, and its first derivative.
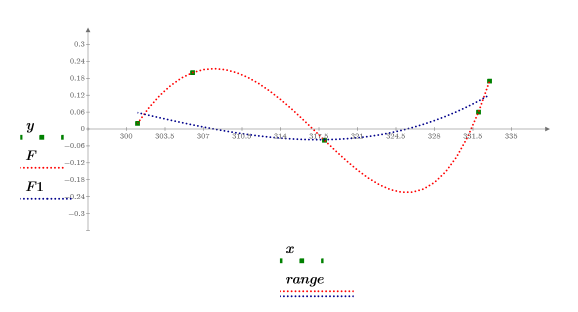
The polycoeff function does not construct the polynomial of best least-squares fit, as is done by the polyfit function.
The results of polyint and polycoeff should not be used to make predictions for y values outside of the range of the original x values.
polyiter
Use the polyiter function to perform a polynomial interpolation.
1. Define the maximum possible number of iterations and the tolerance.
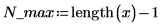
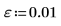
2. Call the polyiter function.
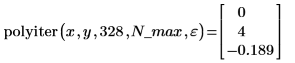
The algorithm did not converge, so it did not stop before the N_max iteration. It did not achieve an error of 0.01 and it returned the same result as polyint:
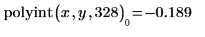
3. Plot the original points, the exact polynomial, and the iterated polynomial.