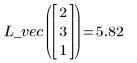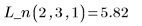Example: Piecewise Quadratic Fitting
Univariate Polynomial Regression
Use the loess function to fit a series of quadratic functions to data using local regression.
1. Define the following matrix:

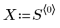
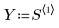
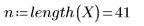
2. Define the span - the percentage of the total number of points in a weighted window around each data point which is used for successive quadratic fits by the loess function.
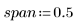
The general guideline is that (span*n) should be >1 since you want the number of points greater than 1 to be averaged into each least-squares weighted fit:
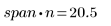
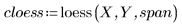
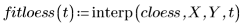
4. Call the polyfit function to fit a second-order polynomial to the data set.
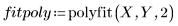
5. Plot the two curves defined above.
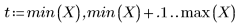
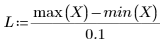
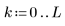
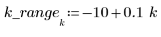
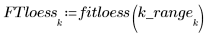
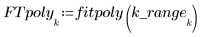
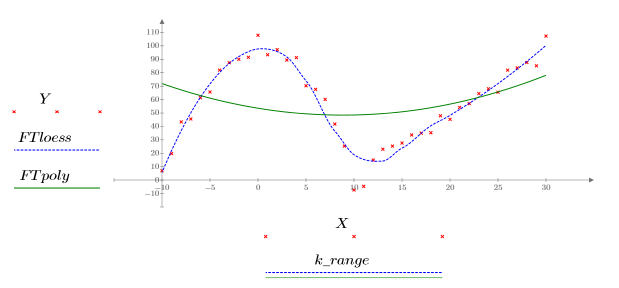
• When the span is large (for example, 2 or 3), the data is considered a single quadratic fit with almost equal weights. The fit approaches the polyfit solution to a quadratic polynomial.
• There are no real exact guidelines for choosing the span. As the span gets larger, the plot of the loess fit gets smoother, because fewer pieces are being connected in the fit. But the fit may fail to follow data features appropriately. Conversely, as the span gets small, you may find that loess does not converge
• The loess algorithm is not designed for extrapolation. If you try to evaluate interp at values beyond the original x-range, an error is returned.
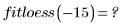
• You may wish to use loess when your data has a somewhat discontinuous characteristic, but when you do not want to piecewise fit by hand, or use complex, physically unrealistic, or nonlinear fitting methods.
Multivariate Polynomial Regression
Use the loess function to perform multivariate polynomial regression. The loess function cannot fit more that 4 independent variables.
1. Define a data set.
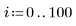
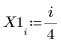
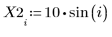
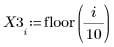
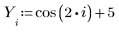
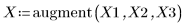
2. Define a smoothing parameter.
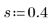
This parameter has the same meaning as for the one-factor case.
3. Call the loess function.
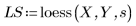
4. Call interp to interpolate multivariate fitting functions. The fitting function can either take a vector of n elements or a set of n arguments, where n is the number of independent factors.
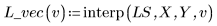
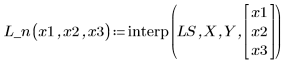
5. Use the fitting functions to predict the value of Y at point (2, 3, 1).