Example: Pareto and Effects Plots
Use Pareto and effects plots to visualize the effects of a design experiment.
1. Call fractfact to construct a fractional factorial design matrix for an experiment testing a painting process. The factors A, B, C, and D stand for the amount of paint, the fluid pressure, the temperature, and the vendor, respectively.
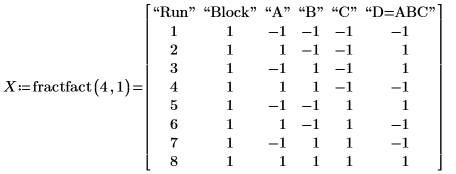
2. Record the results of the experiment in matrix Y. It has one row per run and one column per replicate.
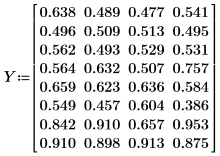
3. Call the quickscreen function to calculate the low and high average response for each factor and for the interactions AB, AC, and BC. For this fractional factorial design, CD, BD, and AD are aliased with AB, AC, and BC, respectively and therefore, they are not included.

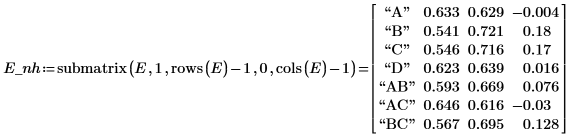
5. Define matrix Data with the factor and the interaction labels in its first column and with the half effects in its second column. Use this matrix as an argument to the pareto function, which returns the label, the half effect, and the cumulative percentage for each factor or interaction. The half effects are returned in descending order.
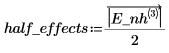
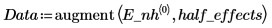

6. View the half effects and the cumulative percentages in a Pareto plot. For the half effects, change the trace type to Column Trace, and add a scaling factor in the unit placeholder so that the size of the half effects matches the size of the cumulative percentages.
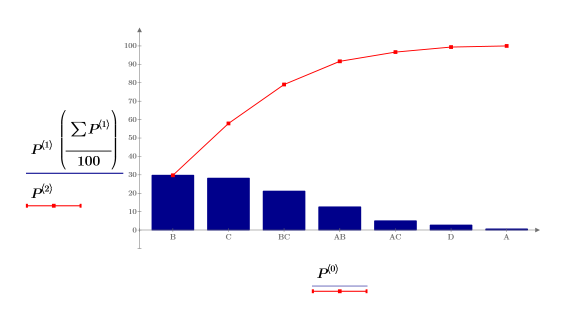
7. Define matrix Paint_Thickness with the low average responses in its first column and the high average responses in its second column. Use this matrix in an effects plot: change the trace type to Effects Trace.
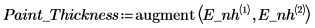
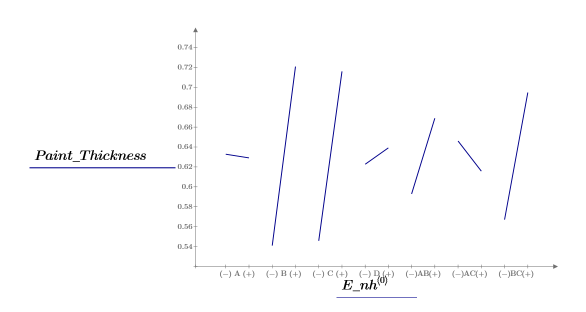
8. According to the Pareto plot and the effects plot, it seems that A, B, and AB are significant factors. However, since AB is aliased with CD, create an effects plot to view the AB interaction and to check if this interaction is important.
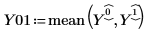 | 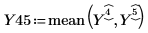 | 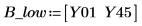 |
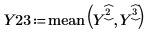 | 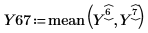 | 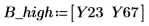 |
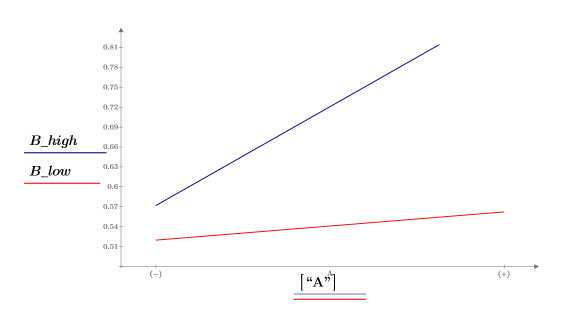
The effects are not parallel, indicating that the interaction AB is important.