Example: Outlier Detection
Use the Grubbs, GrubbsClassic, ThreeSigma, and boxplot functions to find outliers using three different methods to detect outliers.
1. Define a vector that describes the heatflow.
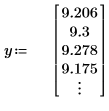
2. Plot the data and the mean of the data.
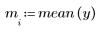
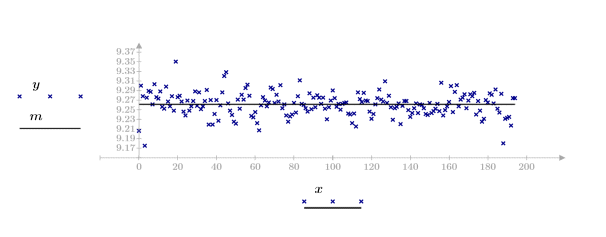
Scatter plots are useful to spot potential outliers, but unless the outliers are severe and infrequent, they can be difficult to detect. You can calculate quantitative metrics for determining which points are outliers.
3. Define the significance level.
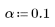
4. Call the Grubbs function to identify the outliers in the data set.
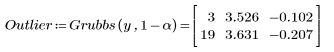
The first column gives the index of each point identified as an outlier (their test statistic exceeds the Grubb's test statistic).
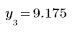
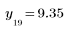
The second column gives the test statistic for each outlier (the distance of the outlier from the mean, in absolute terms).
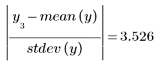
The third column gives the distance of each outlier's test statistic from the Grubbs' test statistic.
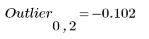
5. Call GrubbsClassic to find the single point most likely to be an outlier.
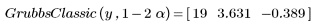
The point with the index value of 19 is the most likely to be an outlier. The columns have the same meaning as those of the matrix returned by the Grubbs function.
6. Call the ThreeSigma function to find the data points which fall outside the 3 sigma region.
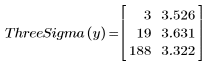
As with the Grubbs function, the first column gives the indices and the second column gives the test statistics of outliers.
The test statistic for each of these data points is greater than 3.
When ThreeSigma does not detect any outliers, the point closest to being an outlier is returned.
7. Call the boxplot function to detect outliers according to the interquartile range method and create a box plot to view the outliers.
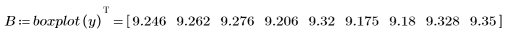
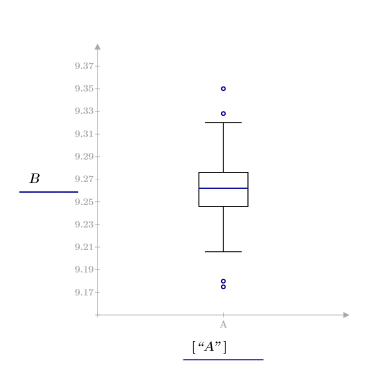
Four outliers were detected using the interquartile range method.
You can also detect outliers after you fit data to a function by using residual analysis.