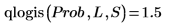Example: Monte Carlo Probability Estimation
Generate random numbers to illustrate how large sampling methods can estimate probabilities of quantities whose distributions are unknown.
1. Set the parameters of a logistic distribution with location and scale parameters L and S.
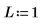
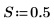
2. Set the Monte Carlo sampling parameters.
◦ Number of individual samples to collect:
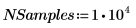
◦ Number of data points in each sample:
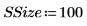
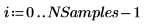
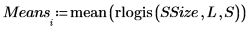
4. Estimate the probability that the mean of a set of random numbers lies within interval [a, b].
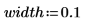
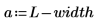
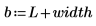
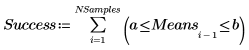
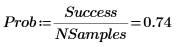
The probability depends on the number of data points in each sample and on the width of the interval.
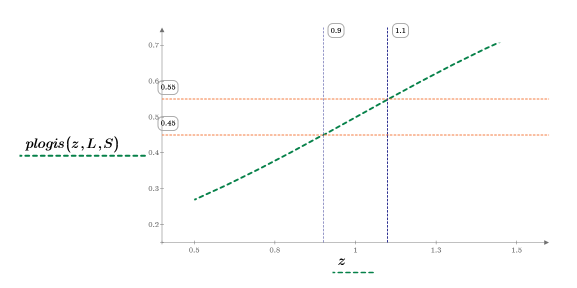
5. Plot the plogis function to show the cumulative probability distribution of the logistic distribution. Use a horizontal marker to mark the probability level.
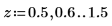
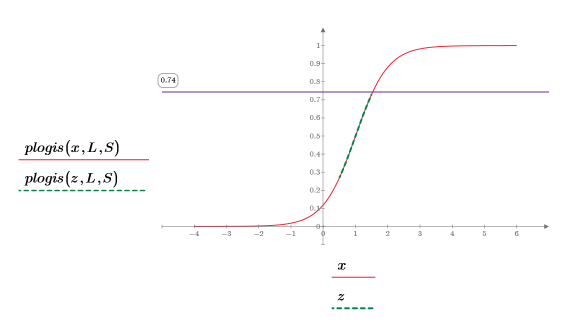
6. Zoom the dashed green segment of the plot and use vertical markers to mark the [a, b] interval and use horizontal markers to mark the lower and upper cumulative probability between [a, b]:
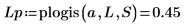
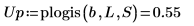
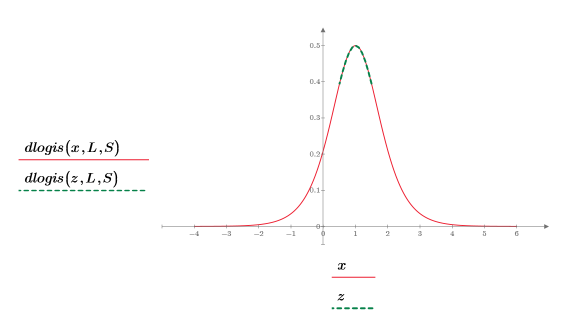
7. Plot the dlogis function to show the probability density of the logistic distribution.
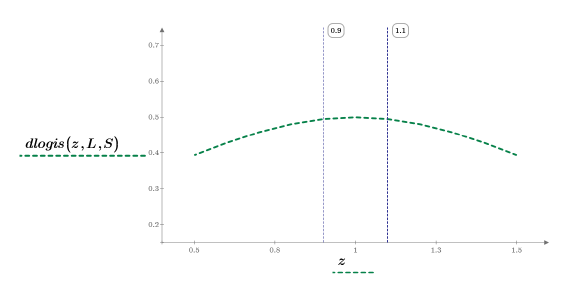
8. Zoom the dashed green segment of the plot and use vertical markers to mark the [a, b] interval:
9. Use function qlogis to calculate the inverse cumulative probability distribution for probability Prob.