Example: Lowpass Filtering Using dftr
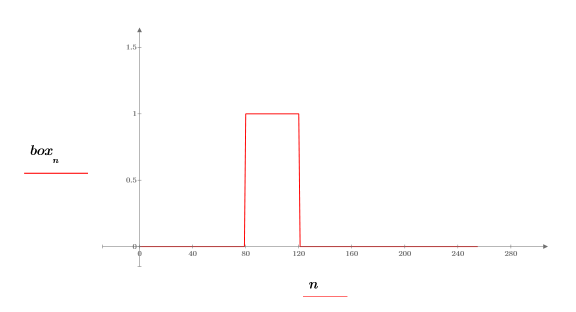
Apply a lowpass Hanning window filter to a boxcar signal by multiplying in the transform domain. The boxcar signal is a single square pulse of width 40 and centered at 100. Sending it through a low-pass filter will smooth its corners.
1. Define the number of sample points.
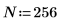
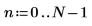
2. Define and plot a boxcar function.
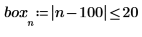
3. Apply the dftr function to the real signal.
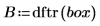
Unlike the dft function which returns the full length conjugate symmetric complex vector, the dftr function returns the first (N/2+1) elements of that vector.
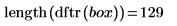
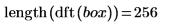
4. Plot the B vector.
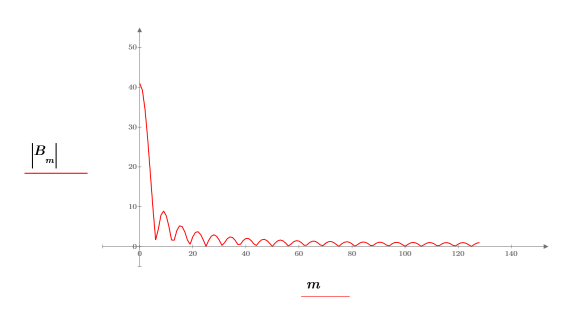
The boxcar transforms to a sinc function.
5. Window this transform with a Hanning window that saves only the low-frequency information.
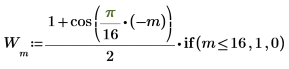
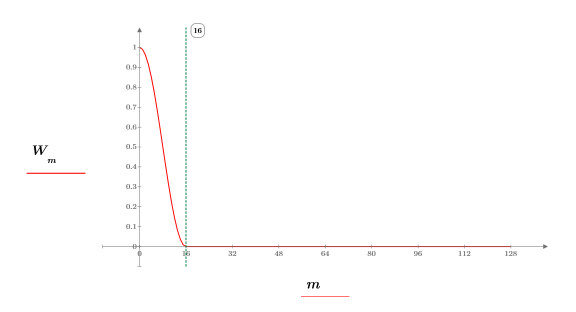
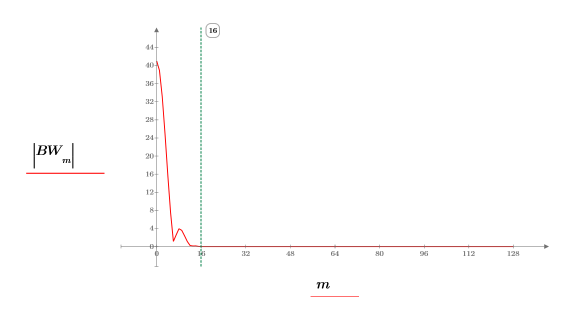
The cos function gives a smooth transition from 1 at the low-frequency end to 0 at the midrange frequency which has been set, in this case, at index 16.
6. Multiply the transformed function by the filtering function.
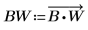
7. Plot the resulting product.
8. Use the idftr function to get the inverse transform of the windowed frequency information.
9. Plot the resulting filtered signal along with the original boxcar signal.
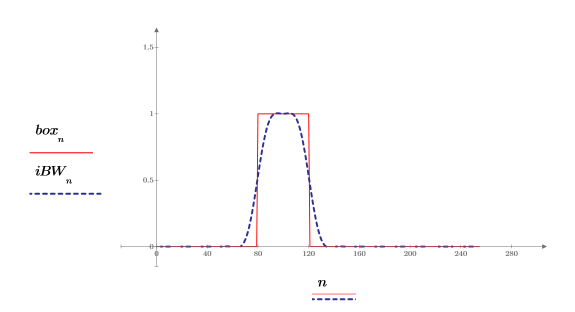
The sharp transitions on the edge of the square pulse, which represent high frequencies, are rounded off and cause the resulting filtered signal to spread out in time.