Example: Local Cosine Transform
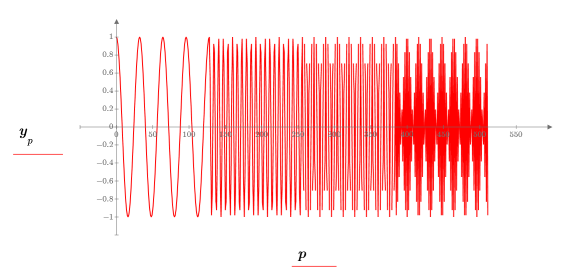
1. Define a test signal by concatenating four sinusoids having four different frequencies.
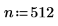 |
|
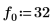 |
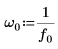 |
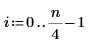 |
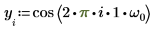 |
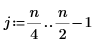 |
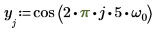 |
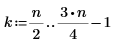 |
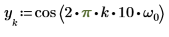 |
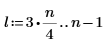 |
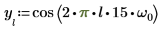 |
2. Plot the test signal.
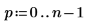
3. Use function cpt to compute the level 2 forward local cosine transform.
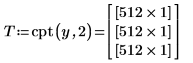
The returned matrix contains the 3 levels of the local cosine transform.
Block at level 0: | 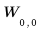 | |||
Block at level 1: | 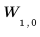 | 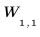 | ||
Block at level 2: | 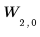 | 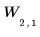 | 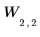 | 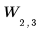 |
4. Plot level 0 of the transform which contains the DCT of the single tapered block of data.
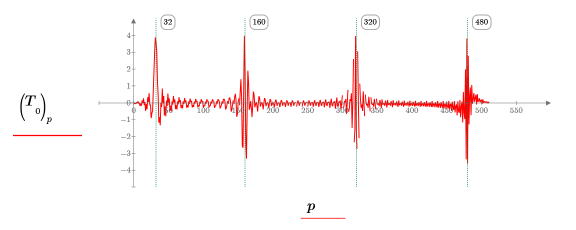
The transform has 4 peaks corresponding to the frequencies of the 4 sinusoids.
5. Plot level 1 of the transform which contains 2 DCT's, one for the first half of the data and one for the second half.
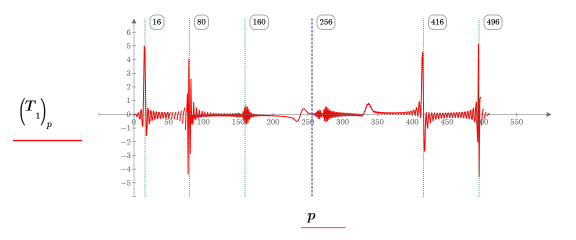
The transform has 2 peaks in each of the two DCT's of n/2 data points. As clicking on the vertical markers shows, the first two are located at half the frequency of the first two sinusoids, and the second two at (n/2) + half the frequency of the second two sinusoids. The blue marker shows the boundary between the two DCT's.
6. Plot level 2 of the transform which contains 4 DCT's, one for each of the four quarters of the data.
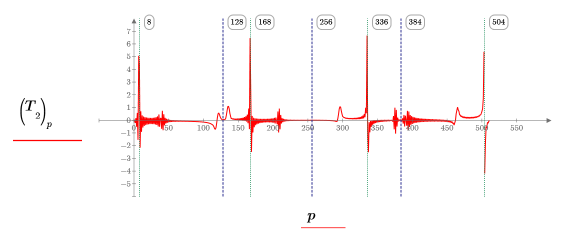
The transform has 1 peak in each of the four DCT's of n/4 data points. As clicking on the vertical markers shows, the first peak is located at quarter the frequency of the first sinusoid, the second peak at n/4 + quarter the frequency of the second sinusoid, the third peak at 2n/4 + quarter the frequency of the third sinusoid and the fourth peak at 3n/4 + quarter the frequency of the fourth sinusoid. The blue markers show the boundaries between the four DCT's.