Example: The Inverse Transformation idft
The idft function is the inverse transform of dft and therefore it is expected to restore the original data input to the complex transform.
Working with Vectors (1D)
1. Define the length of vector v.
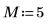
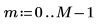
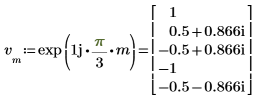
3. Use the dft function to calculate the forward transform of vector v.
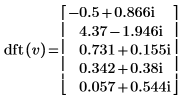
4. Use the idft function to calculate the inverse transform of vector v.

5. Show that the inverse transform of the forward transform of vector v is the original vector v.
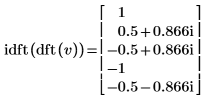 |  |
The results are identical.
Working with Matrices (2D)
1. Define and evaluate matrix C.
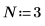
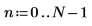
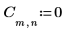
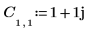
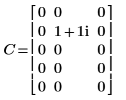
2. Use the dft function to calculate the forward transform of matrix C.

3. Use the idft function to calculate the inverse transform of matrix C.

4. Show that the inverse transform of the forward transform of matrix C is the original matrix C.
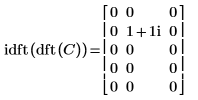 | 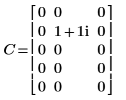 |
The results are identical.
Demonstrating the Underlying Sum Behind idft
One-dimensional Case:
1. Use the exp function and the sum operator to calculate the inverse transform of vector v.
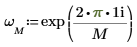
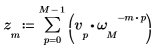
2. Compare the resulting forward transform of vector v with the output of the dft function.
 | 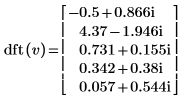 |
The results are identical.
3. Use the sum operator to calculate the inverse transform of vector v.
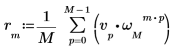
4. Compare the resulting inverse transform of vector v with the output of the idft function.
 |  |
The results are identical.
Two-dimensional case:
1. Use the exp function and the sum operator to calculate the forward transform of matrix C.
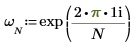
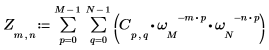
2. Compare the resulting forward transform of matrix C with the output of the dft function.


The results are identical.
3. Use the sum operator to calculate the inverse transform of matrix C.
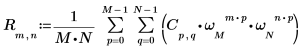
4. Compare the resulting inverse transform of matrix C with the output of the idft function.


The results are identical.