Example: Introduction to FFTs
Fast Fourier transform (FFT) is a numerical method for expressing the frequency content of a set of data measured over time. The data are often continuous, constituting a waveform. To work with the data numerically, they are sampled at regular time intervals at some sample rate. The figures below illustrate some sampled waveforms and the magnitudes of their Fourier transforms plotted against frequency.
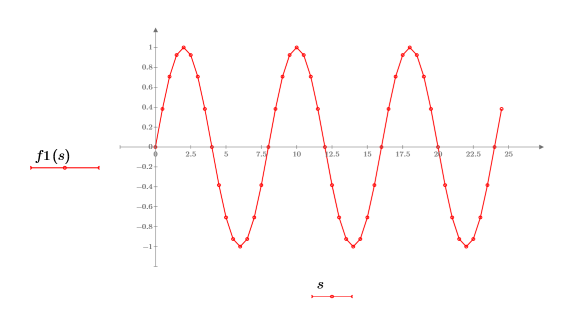
Sampled Sine Waveform
1. Use the sin function to define a sinusoidal waveform.
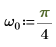
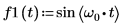
2. Set the number of data points.
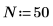
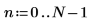
3. Set the distance between samples.
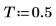
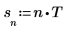
4. Set the sample rate.
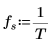
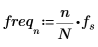
5. Plot the sinusoidal function.
6. Use the dft function to calculate the Discrete Fourier transform.
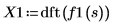
X1 is a vector of real and complex numbers.
7. Find the frequencies at which the peak magnitudes occur.
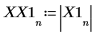
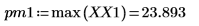
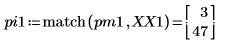
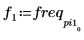
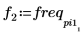
8. Plot the transformed signal and use markers to show the frequency and magnitude of the peaks.
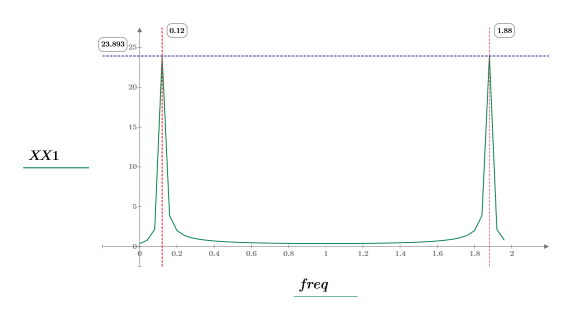
Sampled Cosine Waveform
1. Use the cos function to define a cosine waveform.
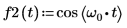
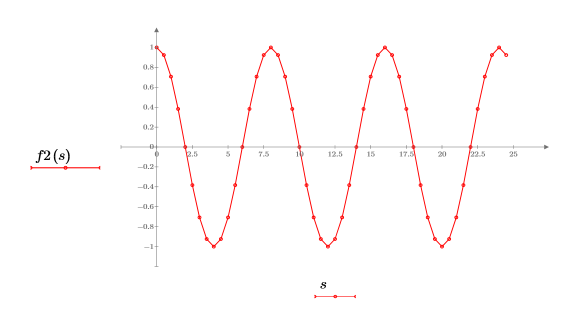
2. Plot the cosine function.
3. Use the dft function to calculate the Discrete Fourier transforms.
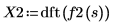
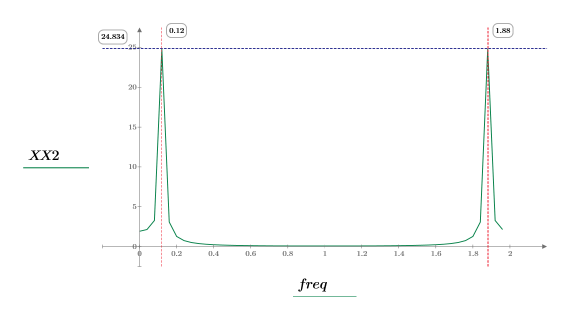
X2 is a vector of real and complex numbers.
4. Find the frequencies at which the maximum magnitudes occur.
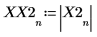
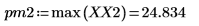
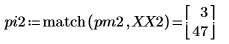
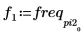
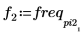
5. Plot the transformed signal and use markers to show the frequency and magnitude of the peaks.
Sampled Exponential Waveform
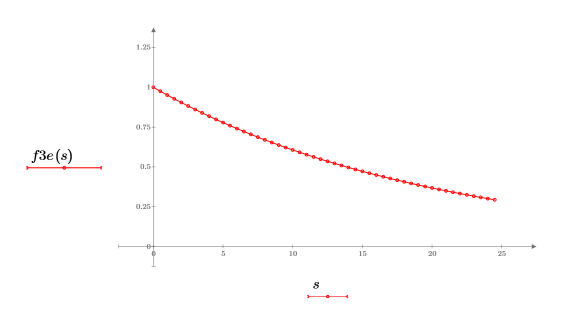
1. Use the exp function to define an exponential waveform.
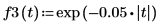
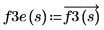
The vectorization operator is used to get the element-wise values of the function because the determinant operator within the definition returns a single scalar value.
2. Plot the exponential function.
3. Use the dft function to calculate the Discrete Fourier transform.
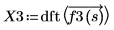
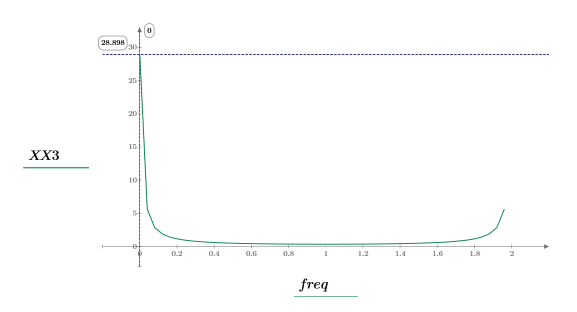
X3 is a vector of real and complex numbers.
4. Find the frequencies at which the maximum magnitudes occur.
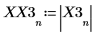
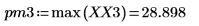
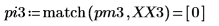
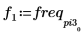
5. Plot the transformed signal and use markers to show the frequency and magnitude of the peaks.
Sampled Step Waveform
1. Use the if function to define a step waveform.
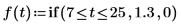
2. Calculate the impulse magnitude at each interval.
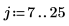
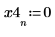
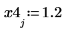
3. Plot the step function.
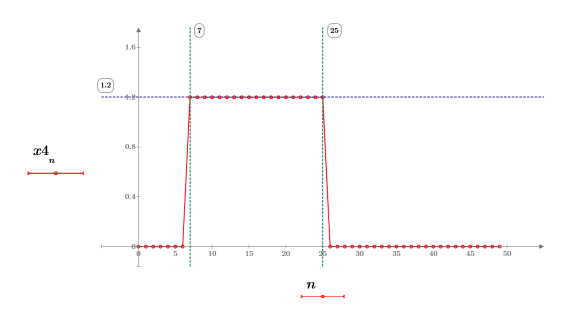
The magnitude is uniform and equals to 1.2 between 7 and 25.
4. Use the dft function to calculate the Discrete Fourier transform.
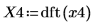
X4 is a vector of real and complex numbers.
5. Find the frequencies at which the maximum magnitudes occur.
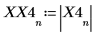
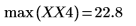
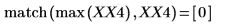
6. Plot the transformed signal and use markers to show the frequency and magnitude of the peaks.
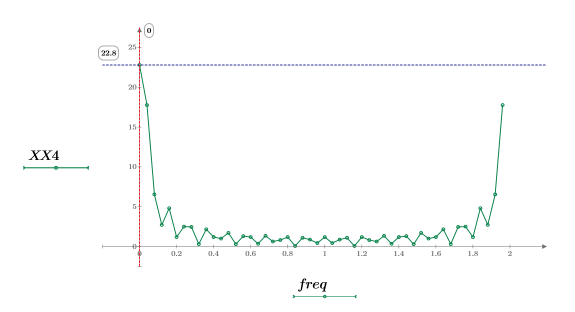
The maximum magnitude occurs at freq0.