Example: Interpolation and Sampling
Use the multirate, resample, and upsample functions to change the sampling rate of a signal in different ways and under different assumptions.
Function multirate with Default FIR Filter
The multirate function uses the group delay of a linear-phase FIR filter to estimate where the initial output transient ends, and truncates.
1. Define the signal parameters.
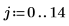 |
|
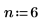 |
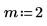 |
2. Use the sin function to define a sum-of-sines signal.
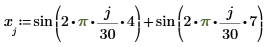
3. Apply the multirate function to the signal.
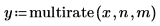
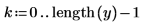
4. Plot the resampled signal.
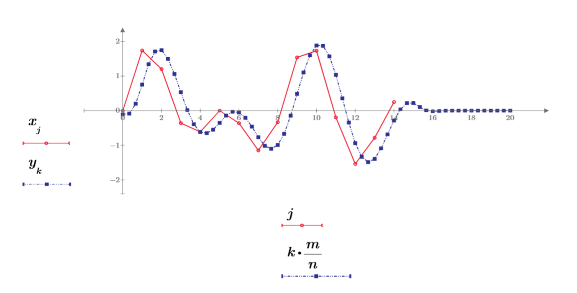
The plot shows that the resampled signal is shifted slightly and contains n/m times the number of original data points. The shift is introduced by the FIR filter and is equal to its group delay.
Function multirate with Optional Lowpass FIR Filter
1. Define the cutoff frequency, the number of coefficients, and the type of taper window.
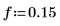 | 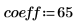 | 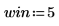 |
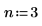 | 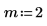 |
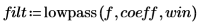
3. Use the multirate function to resample signal x with a different factor.
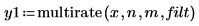
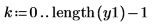
4. Plot the resampled signal.
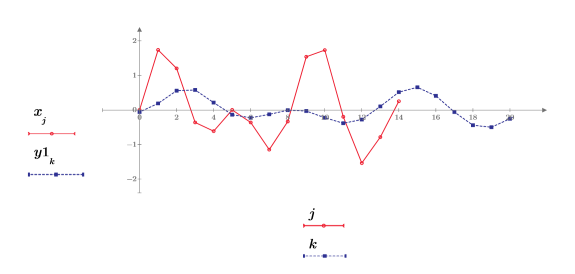
The resampling results in signal attenuation because the FIR filter does not have a gain equal to the upsampling rate n.
5. Adjust the FIR filter coefficients to the correct gain, and replot the resampled signal.
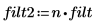
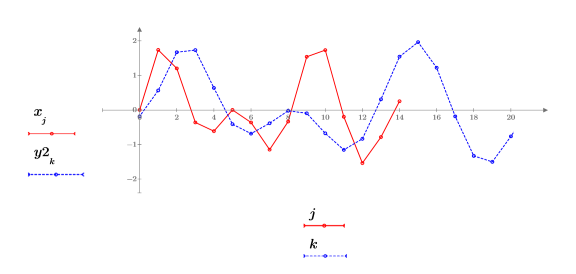
Adjusting the FIR filter coefficients removes the scaling effect.
Signal Upsampling
You can use the multirate function to upsample or downsample a signal.
1. Use the multirate function to upsample signal x by increasing the n/m ratio.
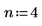 | 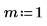 |
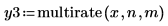 | |
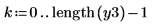 |
2. Plot the upsampled signal.
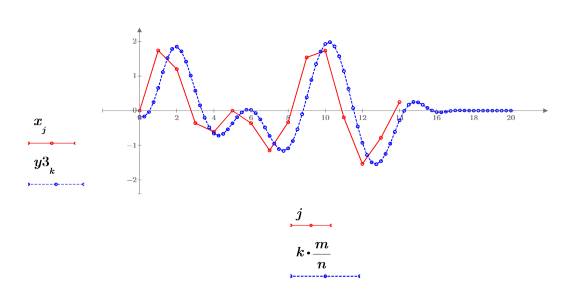
Increasing the n/m ratio results in a higher number of total samples, as seen from the length value, and a higher number of new samples between any two consecutive samples of the original signal.
3. Use the multirate function to downsample signal x by decreasing the n/m ratio.
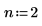 | 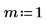 |
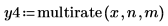 | |
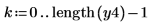 |
4. Plot the downsampled signal.
Decreasing the n/m ratio results in a lower number of total samples, as can be seen from the length value, and a lower number of new samples between any two consecutive samples of the original signal.
Data Upsampling
The upsample function performs an FFT on the original data, adding zeros in the middle of the coefficient range to create a transform that has the required interpolated length, then inverse transforming the extended spectrum. There is no unique method for interpolating data. One might also use a specially designed FIR filter. For regularly behaved data this function returns a reasonable interpolation.
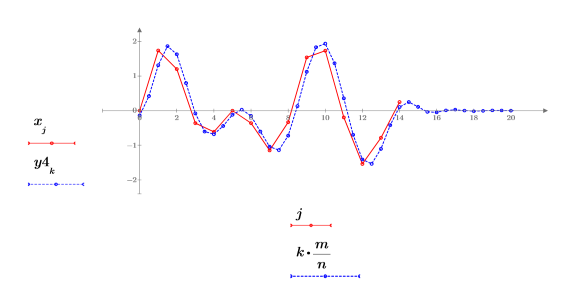
1. Set the interpolation factor n, and apply the upsample function to signal x.
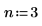
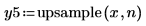
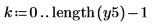
2. Plot the returned signal.
The returned signal is an interpolated version of signal x with n times the number of points.
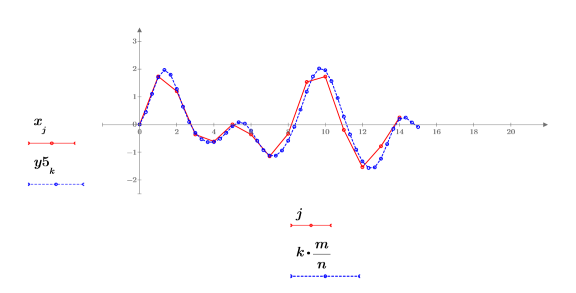
Signal Resampling
The resample function operates by interpolating, as above, to produce n times as many points and then taking every mth point to produce the output.
1. Set the decimation factor m and the interpolation factor n.
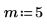 | 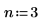 |
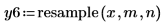 | |
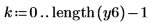 |
2. Plot the returned signal.
The returned signal has 3/5 as many points, so the spacing between samples is 5/3 of the original spacing.
Using upsampling with Aperiodic and Periodic Inputs
The upsample function assumes that the input is periodic. Examine the returned signal in both cases.
Aperiodic Input
1. Set the interpolation factor.
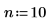
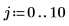
2. Define a non periodic input signal.
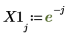
3. Apply the upsample function.
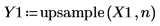
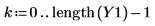
4. Plot the returned signal.
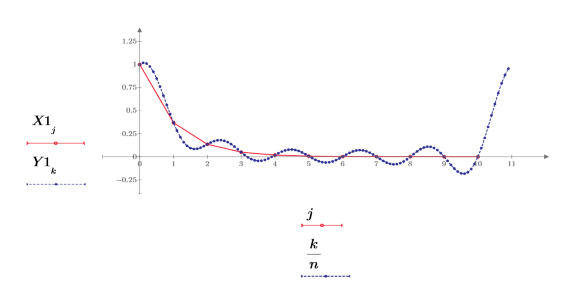
The interpolation routine assumes that X is periodic. Therefore, it tries to interpolate points near the end of the graph that will go back up to the initial height of 1. However, the function gives sensible results if "wrapping" the input sequence gives a reasonably smooth function.
Periodic Input
1. Set the interpolation factor.
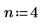
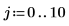
2. Define a periodic input signal.
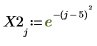
3. Apply the upsample function.
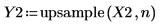
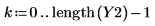
4. Plot the returned signal.
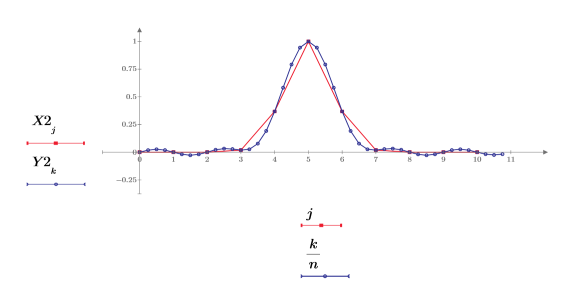
The interpolation is a closer approximation of the original signal when that signal is periodic.