Example: Interactions
Use the effects function to understand the role of interactions in experiments.
1. Use the fullfact function to create a design matrix of two factors.
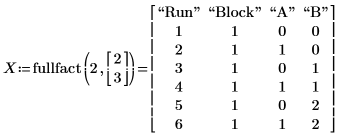
2. Specify the real values for the experiment in matrix Vals. The Gender factor is divided into two levels, male and female. The Age factor is divided into three levels, young, middle, and old. Since the factors do no have the same number of levels, a NaN is inserted in the first row of Vals to fill the empty element.
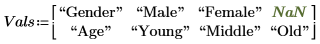
3. Use the doelabel function to sort the results of an experiment according to gender and age.

Matrix X and D are identical, but X shows the coded values of the factors while D shows their real values.
Without Interactions - Only One Significant Factor
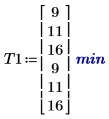
1. Record the average time that each group spends to learn a task. For Run 1, the mean learning time of young male is 9 minutes.
2. Call the effects function to view the effects of gender, age, and their interaction.

The Gender submatrix shows that gender does not influence the learning time. Therefore, there are no interaction effects between age and gender to report upon.
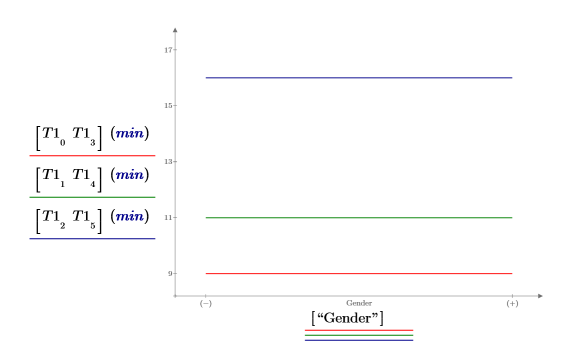
3. Create an effects plot to view how age influences the learning time. The youngest group spends on average 9 minutes to learn the task.
Without Interactions - Two Significant Factors
1. Record the average time that each group spends to learn a second task.
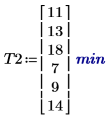
2. Call the effects function to view the effects of gender, age, and their interaction.

The influence of age on the learning process is the same as it was for the first task. This time, however, males spend more time to learn the task than females.
3. To calculate the interaction effects of AB at different levels of A and B, define i and j to be the levels of A and B, and mABi, j to be the mean response for AB at i and j.

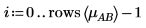
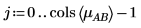
4. Use the mean function to calculate the overall mean for this experiment and the mean for each factor.
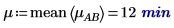
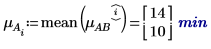
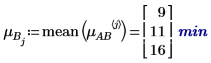
5. Calculate the level effects for each factor.
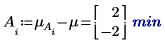
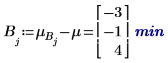
6. For each level of factors A and B, use the augment function to calculate the additive factor effects which are the sum of the overall experiment mean, the level effect of A, and the level effect of B for each levels of A and B.
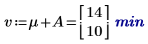
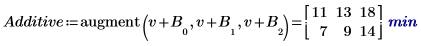
7. Calculate the interaction effects, or the difference between the mean response for AB and the additive factor effect for each levels of A and B.
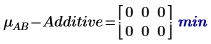
For this task, there are no interaction effects between age and gender.
8. Plot the average learning time for each gender. Young females spend an average of 7 minutes to learn the second task. Because there are no interaction effects between gender and age, the two curves are parallel.
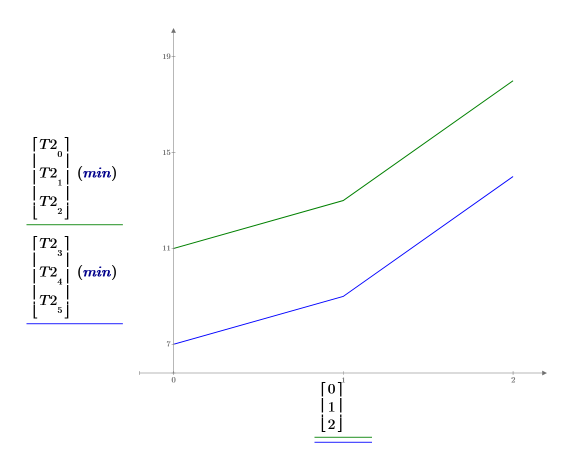
With Important Interactions
1. Record the average time that each group spends to learn a third task. Call the effects function to view the effects of gender, age, and their interaction.
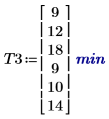

The influence of age is the same as for the first and second tasks, but the influence of gender is smaller than for the second task. For this third task, there are interaction effects between age and gender.
2. Calculate the interaction effects.

3. Use the mean function to calculate the overall mean for this experiment and the mean for each factor.
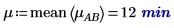
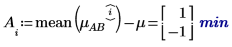
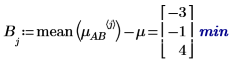
4. For each level of factors A and B, use the augment function to calculate the additive factor effects which are the sum of the overall experiment mean, the level effect of A, and the level effect of B for each levels of A and B.
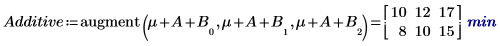
5. Calculate the interaction effects, or the difference between the mean response for AB and the additive factor effect for each levels of A and B.
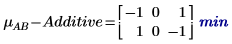
There is a difference between the mean responses of interaction AB and the additive factor effect.
6. Plot the average learning time for each gender. Although there is no difference in performance between young males and females, old males take longer than females to learn the third task. The two curves are not parallel because there is an important interaction between the age and the gender.
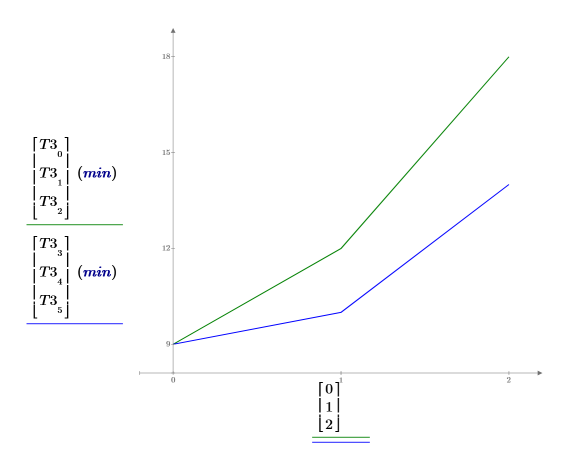
With Unimportant Interactions
1. Record the average time that each group spends to learn a fourth task.

2. Call the effects function to view the effects of gender, age, and their interaction.

The influence of gender and age looks very similar to the third task.
3. Plot the average learning time for each gender. The two curves are almost parallel, indicating that although there is an interaction between age and gender, this interaction is unimportant.
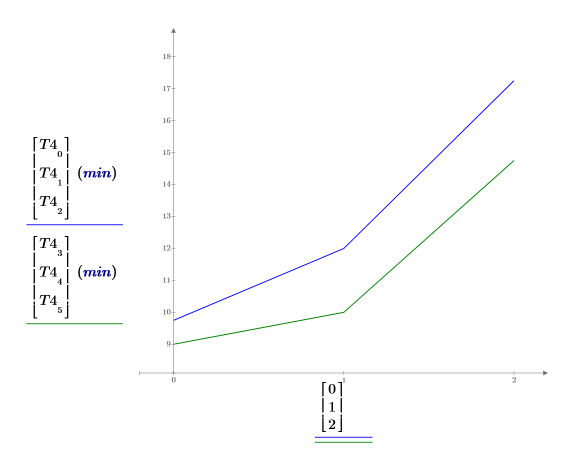
Reference
Neter, J., Kutner, M.H., Nachtsheim, C.J., Wasserman, W., Applied Linear Statistical Models, 4th ed., McGraw-Hill/Irwin, Boston, 1996, pp. 803.