Example: Hypothesis Test of a Normal Mean
Use the normal distribution functions to conduct a hypothesis test for normal, independent data.
1. Define the following vector of data.

2. Use functions length and mean to collect the sample statistics.
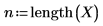
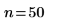
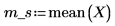
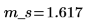
The sample mean is m_s. |
3. Define the significance level α, the population standard deviation σ and the proposed population mean μ.
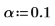
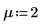
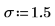
4. Calculate the Z score.
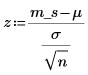
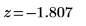
Two-Tailed Test
1. State the null and the alternative hypothesis for a two-tailed test.
H0: m = μ
H1: m ≠ μ
2. Use function pnorm to test the hypothesis in terms of p-values for the two-tailed test. In this example, all of the Boolean expressions evaluate to 1 when the null hypothesis is true (you do not reject H0).

The comparison between the p-value and the significance level indicates there is evidence that the alternative hypothesis is true.
3. Use function qnorm to test the hypothesis in terms of q-values for the two-tailed test.
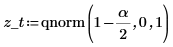
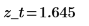
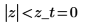
Reject the null hypothesis. There is evidence that the mean is significantly different from μ.
4. Use function dnorm to calculate the standard normal distribution.
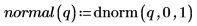
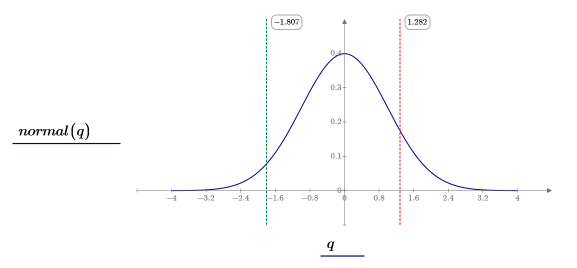
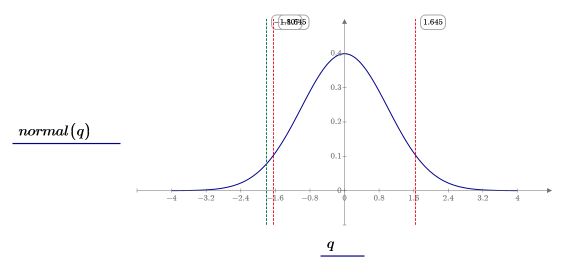
5. Plot the normal distribution and then use red markers to show the left and right boundaries of the critical region. Use a green marker to show the Z score.
Left-Tailed Test
1. State the null and the alternative hypothesis for a left-tailed test.
H0: m >= μ
H1: m < μ
2. Use function pnorm to test the hypothesis in terms of p-values for the left-tailed test.
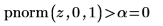
The comparison between the p-value and the significance level indicates there is evidence that the alternative hypothesis is true.
3. Use function qnorm to test the hypothesis in terms of q-values for the left-tailed test.
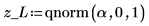
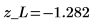
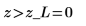
Reject the null hypothesis. There is evidence that the mean is smaller than μ.
4. Plot the standard normal distribution and then use a red marker to show the left boundary of the critical region. Use a green marker to show the Z score.
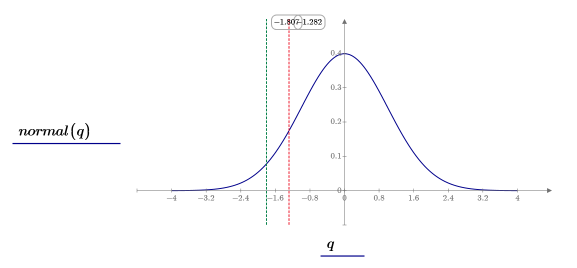
Right-Tailed Test
1. State the null and the alternative hypothesis for a right-tailed test.
H0: m <= μ
H1: m > μ
2. Use the pnorm function to test the hypothesis in terms of p-values for the right-tailed test:
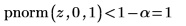
The comparison between the p-value and the significance level indicates there is no evidence that the alternative hypothesis is true.
3. Use the qnorm function to test the hypothesis in terms of q-values for the right-tailed test.
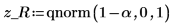
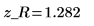
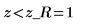
Accept the null hypothesis. There is no evidence that the mean is greater than μ.
4. Plot the standard normal distribution and then use a red marker to show the right boundary of the critical region. Use a green marker to show the Z score.