Example: Grubbs' Method for Detecting Outliers

Functions > Data Analysis > Outliers and NaN > Example: Grubbs' Method for Detecting Outliers

Grubbs' Test Statistic

Calculate the Grubb's test statistic, as used by the Grubbs function, to detect outliers. Compare the Grubb's test statistic with the test statistic of the ouliers.

1. Define a data set describing a heatflow experiment and plot it.

<region id="ID0ECCSU" top="326.40000000000003" left="19.200000000000003" height="235.157894736842" width="561.473684210526" xmlns="http://schemas.mathsoft.com/worksheet50">
  <plot origin-positioning="true">
    <xyPlot>
      <title class="- topic/title " wwtype:type="Paragraph" xmlns:wwtype="urn:WebWorks-Type-Schema" />
      <legend />
      <traces>
        <trace resultRef="58">
          <traceStyle color="#FF00008B" symbol="x" line-weight="1" line-style="None">lines</traceStyle>
        </trace>
        <trace resultRef="59">
          <traceStyle color="#FF000000" symbol="none" line-weight="1" line-style="Solid">lines</traceStyle>
        </trace>
      </traces>
      <graph-size width="461.473684210526" height="177.557894736842" />
      <axes>
        <xAxis rank="1" legend-position="PlotBoundaryBottom" start="0" end="200">
          <axisLine position="bottom" positionticmark="-1" legendWidth="92.1466666666667" />
          <axisGrid>
            <gridFrequency>11</gridFrequency>
            <gridLabels display="true" />
            <gridLines />
            <tickMarks display="true" />
          </axisGrid>
          <axisLabel />
          <markers />
          <numberFormat>
            <decimal precision="3" show-trailing-zeros="false" radix="dec" imaginary-value="i" />
          </numberFormat>
          <plotEquations>
            <plotEquation>
              <math resultRef="60">
                <id xml:space="preserve" xmlns="http://schemas.mathsoft.com/math50">range</id>
              </math>
              <math resultRef="61">
                <placeholder xmlns="http://schemas.mathsoft.com/math50" />
              </math>
            </plotEquation>
          </plotEquations>
          <xyDomain scale-type="linear" auto-scale="true">
            <startValue>
              <placeholder xmlns="http://schemas.mathsoft.com/math50" />
            </startValue>
            <endValue>
              <placeholder xmlns="http://schemas.mathsoft.com/math50" />
            </endValue>
          </xyDomain>
        </xAxis>
        <yAxis rank="1" legend-position="PlotBoundaryLeft" start="9.175" end="9.355">
          <axisLine position="origin" positionticmark="0" legendWidth="66.1366666666667" />
          <axisGrid>
            <gridFrequency>13</gridFrequency>
            <gridLabels display="true" />
            <gridLines />
            <tickMarks display="true" />
          </axisGrid>
          <axisLabel />
          <markers />
          <numberFormat>
            <decimal precision="3" show-trailing-zeros="false" radix="dec" imaginary-value="i" />
          </numberFormat>
          <plotEquations>
            <plotEquation>
              <math resultRef="62">
                <id xml:space="preserve" xmlns="http://schemas.mathsoft.com/math50">y</id>
              </math>
              <math resultRef="63">
                <placeholder xmlns="http://schemas.mathsoft.com/math50" />
              </math>
            </plotEquation>
            <plotEquation>
              <math resultRef="64">
                <id xml:space="preserve" xmlns="http://schemas.mathsoft.com/math50">m</id>
              </math>
              <math resultRef="65">
                <placeholder xmlns="http://schemas.mathsoft.com/math50" />
              </math>
            </plotEquation>
          </plotEquations>
          <xyDomain scale-type="linear" auto-scale="true">
            <startValue>
              <placeholder xmlns="http://schemas.mathsoft.com/math50" />
            </startValue>
            <endValue>
              <placeholder xmlns="http://schemas.mathsoft.com/math50" />
            </endValue>
          </xyDomain>
        </yAxis>
      </axes>
    </xyPlot>
  </plot>
</region>

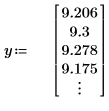
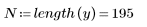
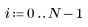
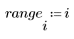
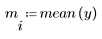
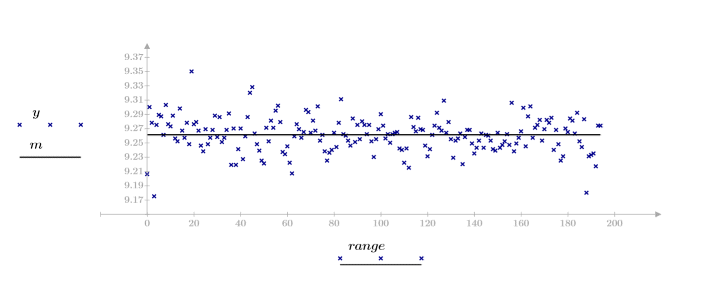
2. Define the critical value of the Student's t-distribution with N - 2 degrees of freedom and a significance level of alpha/(2N).

<region id="ID0E1DSU" top="652.80000000000007" left="19.200000000000003" height="47.2" width="197.51" xmlns="http://schemas.mathsoft.com/worksheet50">
  <math resultRef="72">
    <define xmlns="http://schemas.mathsoft.com/math50">
      <function>
        <id labels="*" xml:space="preserve">t</id>
        <boundVars>
          <id labels="*" xml:space="preserve">alpha</id>
        </boundVars>
      </function>
      <apply>
        <id labels="FUNCTION" xml:space="preserve" label-is-contextual="true">qt</id>
        <sequence>
          <apply>
            <div />
            <id labels="VARIABLE" xml:space="preserve" label-is-contextual="true">alpha</id>
            <apply>
              <mult />
              <real>2</real>
              <id labels="VARIABLE" xml:space="preserve" label-is-contextual="true">N</id>
            </apply>
          </apply>
          <apply>
            <minus />
            <id labels="VARIABLE" xml:space="preserve" label-is-contextual="true">N</id>
            <real>2</real>
          </apply>
        </sequence>
      </apply>
    </define>
    <resultFormat>
      <decimal precision="3" show-trailing-zeros="false" radix="dec" imaginary-value="i" />
      <matrix size="12,12" offset="0,0" show-indices="false" expand-nested-arrays="false" />
    </resultFormat>
  </math>
</region>

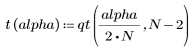
The function qt calculates the inverse cumulative probability density of the Student's t distribution.

3. Define the Grubbs' test statistic as a function of alpha.

<region id="ID0EXGSU" top="748.80000000000007" left="19.200000000000003" height="66.865333527326584" width="299.03933330357074" xmlns="http://schemas.mathsoft.com/worksheet50">
  <math resultRef="74">
    <define xmlns="http://schemas.mathsoft.com/math50">
      <function>
        <id labels="*" xml:space="preserve">crit</id>
        <boundVars>
          <id labels="*" xml:space="preserve">alpha</id>
        </boundVars>
      </function>
      <apply>
        <mult />
        <apply>
          <div />
          <apply>
            <minus />
            <id labels="VARIABLE" xml:space="preserve" label-is-contextual="true">N</id>
            <real>1</real>
          </apply>
          <apply>
            <nthRoot />
            <placeholder />
            <id labels="VARIABLE" xml:space="preserve" label-is-contextual="true">N</id>
          </apply>
        </apply>
        <parens>
          <apply>
            <nthRoot />
            <placeholder />
            <apply>
              <div />
              <apply>
                <pow />
                <apply>
                  <id labels="VARIABLE" xml:space="preserve" label-is-contextual="true">t</id>
                  <id labels="VARIABLE" xml:space="preserve" label-is-contextual="true">alpha</id>
                </apply>
                <real>2</real>
              </apply>
              <apply>
                <plus />
                <apply>
                  <minus />
                  <id labels="VARIABLE" xml:space="preserve" label-is-contextual="true">N</id>
                  <real>2</real>
                </apply>
                <apply>
                  <pow />
                  <apply>
                    <id labels="VARIABLE" xml:space="preserve" label-is-contextual="true">t</id>
                    <id labels="VARIABLE" xml:space="preserve" label-is-contextual="true">alpha</id>
                  </apply>
                  <real>2</real>
                </apply>
              </apply>
            </apply>
          </apply>
        </parens>
      </apply>
    </define>
    <resultFormat>
      <decimal precision="3" show-trailing-zeros="false" radix="dec" imaginary-value="i" />
      <matrix size="12,12" offset="0,0" show-indices="false" expand-nested-arrays="false" />
    </resultFormat>
  </math>
</region>

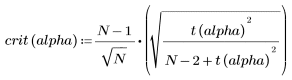
4. Define the level of significance for a confidence level of 90%.

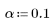
5. Call the Grubbs function to detect outliers.

<region id="ID0E2JSU" top="864.00000000000011" left="19.200000000000003" height="44.2" width="339.71999999999997" xmlns="http://schemas.mathsoft.com/worksheet50">
  <math resultRef="78">
    <define xmlns="http://schemas.mathsoft.com/math50">
      <id labels="*" xml:space="preserve">outlier</id>
      <eval>
        <apply>
          <id labels="FUNCTION" xml:space="preserve" label-is-contextual="true">Grubbs</id>
          <sequence>
            <id labels="VARIABLE" xml:space="preserve" label-is-contextual="true">y</id>
            <apply>
              <minus />
              <real>1</real>
              <id labels="VARIABLE" xml:space="preserve" label-is-contextual="true">α</id>
            </apply>
          </sequence>
        </apply>
        <unitOverride>
          <placeholder />
        </unitOverride>
      </eval>
    </define>
    <resultFormat>
      <decimal precision="3" show-trailing-zeros="false" radix="dec" imaginary-value="i" />
      <matrix size="12,12" offset="0,0" show-indices="false" expand-nested-arrays="false" />
    </resultFormat>
  </math>
</region>

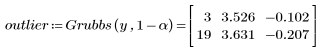
The Grubbs function can accept a matrix as an input, in which case it returns nested pairs of indices for the array locations of the outliers.

6. Compare the Grubb's test statistic with the test statistics of the outliers.

The two outliers have a test statistic greater than the Grubb's test statistic. Even if more than one index is returned, this does not mean that all candidates must be outliers. This is because the critical value and the test statistic change if a candidate is removed. Both are dependent on N.

Because the Grubb’s test assumes that the data is normal, it is worth to check that your data follows a normal distribution. For example, you can use a visual test such as the normal probability plot before proceeding.

GrubbsClassic

Use the GrubbsClassic function to find the point which is the most likely to be an outlier in a data set.

1. Calculate the test statistic which is the greatest for the above data set.

<region id="ID0EVOSU" top="1286.4" left="38.400000000000006" height="51.2" width="267.96333333333337" xmlns="http://schemas.mathsoft.com/worksheet50">
  <math resultRef="82">
    <define xmlns="http://schemas.mathsoft.com/math50">
      <id labels="*" xml:space="preserve">Gmax</id>
      <eval>
        <apply>
          <div />
          <apply>
            <id labels="FUNCTION" xml:space="preserve" label-is-contextual="true">max</id>
            <apply>
              <vectorize />
              <apply>
                <absval />
                <apply>
                  <minus />
                  <id labels="VARIABLE" xml:space="preserve" label-is-contextual="true">y</id>
                  <apply>
                    <id labels="FUNCTION" xml:space="preserve" label-is-contextual="true">mean</id>
                    <id labels="VARIABLE" xml:space="preserve" label-is-contextual="true">y</id>
                  </apply>
                </apply>
              </apply>
            </apply>
          </apply>
          <apply>
            <id labels="FUNCTION" xml:space="preserve" label-is-contextual="true">stdev</id>
            <id labels="VARIABLE" xml:space="preserve" label-is-contextual="true">y</id>
          </apply>
        </apply>
        <unitOverride>
          <placeholder />
        </unitOverride>
      </eval>
    </define>
    <resultFormat>
      <decimal precision="3" show-trailing-zeros="false" radix="dec" imaginary-value="i" />
      <matrix size="12,12" offset="0,0" show-indices="false" expand-nested-arrays="false" />
    </resultFormat>
  </math>
</region>

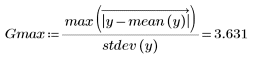
2. Define alpha for a 98% confidence interval.

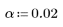
3. Compare the Grubbs' test statistic with Gmax.

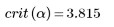
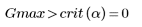
No outliers are detected at this significance level.

4. Call the GrubbsClassic function.

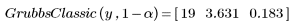
The point returned by GrubbsClassic is not an outlier, but it is the data point which is the most likely to be an outlier.

The Limiting Probability of Detecting Outliers

Use the special construct root to calculate the limiting probability at which outliers are detected.

<region id="ID0EYVSU" top="1670.4000000000003" left="38.400000000000006" height="25.6" width="302.86" xmlns="http://schemas.mathsoft.com/worksheet50">
  <math resultRef="92">
    <define xmlns="http://schemas.mathsoft.com/math50">
      <id labels="VARIABLE" xml:space="preserve">α_limit</id>
      <eval>
        <apply>
          <id labels="KEYWORD" xml:space="preserve">root</id>
          <sequence>
            <apply>
              <minus />
              <apply>
                <id labels="VARIABLE" xml:space="preserve" label-is-contextual="true">crit</id>
                <id labels="VARIABLE" xml:space="preserve" label-is-contextual="true">α</id>
              </apply>
              <id labels="VARIABLE" xml:space="preserve" label-is-contextual="true">Gmax</id>
            </apply>
            <id labels="VARIABLE" xml:space="preserve" label-is-contextual="true">α</id>
          </sequence>
        </apply>
        <unitOverride>
          <placeholder />
        </unitOverride>
      </eval>
    </define>
    <resultFormat>
      <decimal precision="3" show-trailing-zeros="false" radix="dec" imaginary-value="i" />
      <matrix size="12,12" offset="0,0" show-indices="false" expand-nested-arrays="false" />
    </resultFormat>
  </math>
</region>

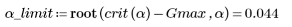
Outliers are detected when alpha is bigger than α_limit, or in other words, when the confidence interval is smaller than (1 - α_limit):

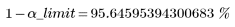
This is consistent with the above findings. No outliers were detected for a 98% confidence interval, but two outliers were detected for a 90% confidence interval.