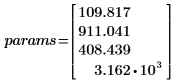Example: Gradient Operator
• Define a function f:
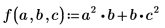
Use the gradient operator to receive a vector of partial derivatives for f:
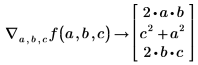
• Define a vector function and calculate the gradient of the function f by vector x.
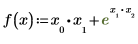

In this example, ORIGIN, which sets the starting index for all arrays, is set to 0.
The variable with the largest subscript in f is x2. Mathcad assumes that there are three variables, x0, x1, and x2. The results a gradient vector of three values containing the partial derivatives of these variables. If either x0 or x1 did not appear in f, Mathcad still returns a vector of three values, but the entries corresponding to the missing variables are set to 0.
For the largest subscript appearing in f, n, Mathcad assumes n + 1 variables, x0, x1, ... xn, and returns a vector of length n + 1.
• If you define x numerically, you can evaluate the gradient with the equal sign =. Mathcad evaluates the gradient at the values in x and returns a vector of numbers, representing the gradient at the point x. The length of x must be greater than the largest subscript appearing in f, and Mathcad returns a gradient with length(x) entries.
In the following example, x0 and x1 are the only variables appearing in the expression, Mathcad takes the partial derivatives with respect to x0 and x1 and returns a vector of two values.
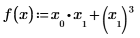
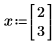
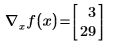
However, if you define x to be a three-element vector, Mathcad assumes that there is an additional variable, x2, which does not appear in the expression. The results is a vector of three elements.
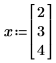
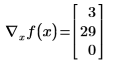
Using Gradient Operator with genfit Function
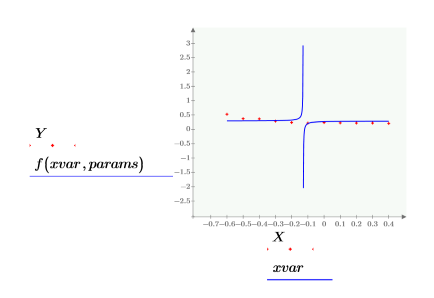
The gradient operator is particularly useful for setting up the arguments to the genfit function, which fits a general, nonlinear function to a data set.
• Use the data in the following table.
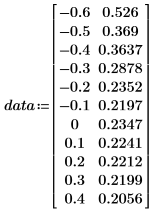
• The first column contains the x-values of the data, and the second column contains the y-values.
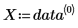
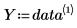
• Model the data by a function of the following form:
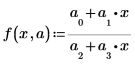
Here, a1, a2 and a3 are unknown parameters contained in vector a
You can model the data by calling genfit as follows:
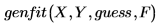
In this expression
◦ X and Y are vectors containing the x-values and the y-values of the data.
◦ guess is a vector of initial guess values for the parameters.
◦ F is a vector whose first entry is the model function f(x, a), and whose remaining entries are the partial derivatives of f with respect to the unknown parameters.
• Create the vector F using the gradient operator and the stack function.
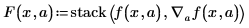

• The stack function puts the model function f on top of the vector of partial derivatives created by the gradient operator.
• Next, create a guess vector for the parameters.
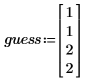
• Apply genfit as follows:
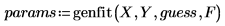
• The parameters that give the best fit are: