Example: Fitting a Model Function to Data
Test how well your data is modeled by a linear, quadratic, or exponential function.
1. Define a data set.
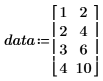
2. Capture column 0 and column 1 into separate vectors.
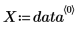
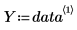
Linear Fit
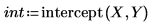
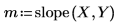
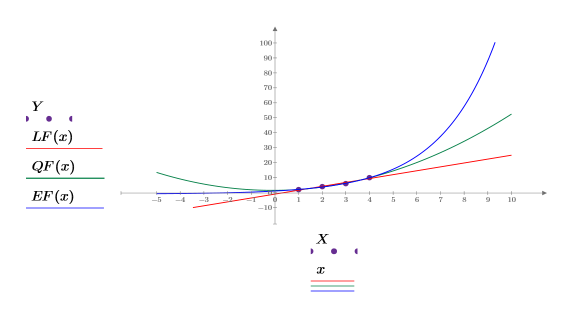
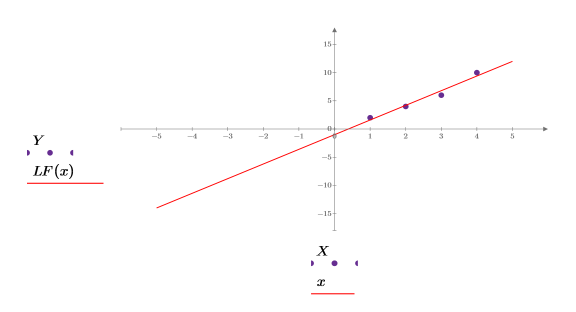
2. Plot the linear fitting function LF along with X and Y.
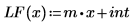
Quadratic Fit
1. Set the polynomial order.
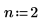
2. Use the polyfit function to calculate the fitting function.
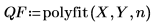
◦ Previous versions of this example used the deprecated regress function to obtain a matrix of coefficients which is then passed to the interp function to obtain the fitting function.
◦ The polyfit function, recommended as an alternate to the deprecated regress function, returns the fitting function and thus there is no longer a need for using the interp function.
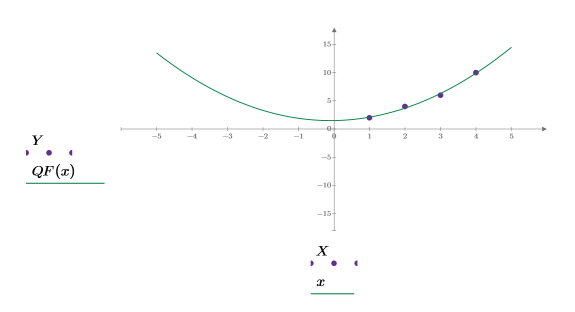
◦ As an experiment, change the value of the polynomial order to see its effect on the fitting function as seen in the below plot.
3. Plot the quadratic fitting function QF.
Exponential Fit
The exponential fitting function is represented by:
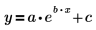
1. Provide guess values for parameters a, b, and c.
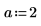 | 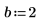 | 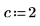 |
2. Define the guess vector.
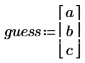
3. Use the expfit function to calculate the three coefficients of the exponential curve.
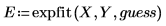
4. Plot the exponential fitting function EF.
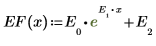
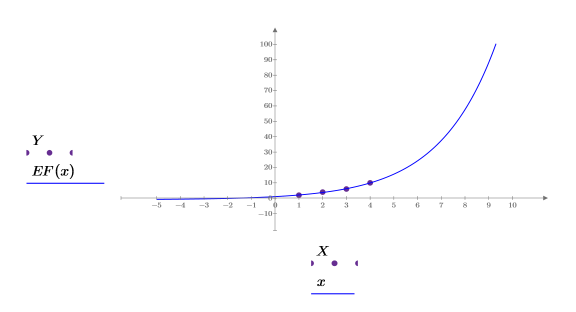
5. View the three plots to see how well each fitting model fits the data.