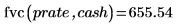Example: Finance Functions

Functions > Finance > Example: Finance Functions

1. Define an annual interest rate:

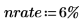
2. Define the number of compounding periods per year:

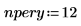
3. Define a periodic interest rate:

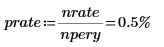
4. Define a number of compounding periods:

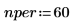
5. Define the present and future values of a loan:

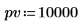
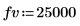
Payment

1. Use the pmt function to calculate the required monthly payment to pay off a 10,000 loan, at 6%, over a period of 5 years:

<region id="ID0ELRDX" top="614.40000000000009" left="38.400000000000006" height="25.6" width="284.26333333333332" xmlns="http://schemas.mathsoft.com/worksheet50">
  <math resultRef="62">
    <define xmlns="http://schemas.mathsoft.com/math50">
      <id labels="VARIABLE" xml:space="preserve">PMT</id>
      <eval>
        <apply>
          <id labels="FUNCTION" xml:space="preserve" label-is-contextual="true">pmt</id>
          <sequence>
            <id labels="VARIABLE" xml:space="preserve" label-is-contextual="true">prate</id>
            <id labels="VARIABLE" xml:space="preserve" label-is-contextual="true">nper</id>
            <id labels="VARIABLE" xml:space="preserve" label-is-contextual="true">pv</id>
          </sequence>
        </apply>
        <unitOverride>
          <placeholder />
        </unitOverride>
      </eval>
    </define>
    <resultFormat>
      <general precision="2" show-trailing-zeros="false" radix="dec" zero-threshold="15" imaginary-value="i" exponential-threshold="3" />
    </resultFormat>
  </math>
</region>

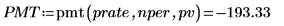
Payments toward a loan are entered and displayed as negative numbers.

2. Use the ppmt function to calculate the 36th principal-only payment of the above loan:

<region id="ID0EEUDX" top="768.00000000000011" left="38.400000000000006" height="25.6" width="403.29666666666674" xmlns="http://schemas.mathsoft.com/worksheet50">
  <math resultRef="66">
    <define xmlns="http://schemas.mathsoft.com/math50">
      <id labels="VARIABLE" xml:space="preserve">PRINCIPAL</id>
      <eval>
        <apply>
          <id labels="FUNCTION" xml:space="preserve">ppmt</id>
          <sequence>
            <id labels="VARIABLE" xml:space="preserve" label-is-contextual="true">prate</id>
            <id labels="VARIABLE" xml:space="preserve" label-is-contextual="true">nthpay</id>
            <id labels="VARIABLE" xml:space="preserve" label-is-contextual="true">nper</id>
            <id labels="VARIABLE" xml:space="preserve" label-is-contextual="true">pv</id>
          </sequence>
        </apply>
        <unitOverride>
          <placeholder />
        </unitOverride>
      </eval>
    </define>
    <resultFormat>
      <general precision="2" show-trailing-zeros="false" radix="dec" zero-threshold="15" imaginary-value="i" exponential-threshold="3" />
    </resultFormat>
  </math>
</region>

3. Use the ipmt function to calculate the 36th interest-only payment of the above loan:

<region id="ID0ELWDX" top="844.80000000000018" left="38.400000000000006" height="25.6" width="384.40666666666669" xmlns="http://schemas.mathsoft.com/worksheet50">
  <math resultRef="68">
    <define xmlns="http://schemas.mathsoft.com/math50">
      <id labels="VARIABLE" xml:space="preserve">INTEREST</id>
      <eval>
        <apply>
          <id labels="FUNCTION" xml:space="preserve" label-is-contextual="true">ipmt</id>
          <sequence>
            <id labels="VARIABLE" xml:space="preserve" label-is-contextual="true">prate</id>
            <id labels="VARIABLE" xml:space="preserve" label-is-contextual="true">nthpay</id>
            <id labels="VARIABLE" xml:space="preserve" label-is-contextual="true">nper</id>
            <id labels="VARIABLE" xml:space="preserve" label-is-contextual="true">pv</id>
          </sequence>
        </apply>
        <unitOverride>
          <placeholder />
        </unitOverride>
      </eval>
    </define>
    <resultFormat>
      <general precision="2" show-trailing-zeros="false" radix="dec" zero-threshold="15" imaginary-value="i" exponential-threshold="3" />
      <matrix size="12,12" offset="0,0" show-indices="false" expand-nested-arrays="false" />
    </resultFormat>
  </math>
</region>

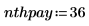
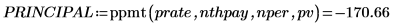
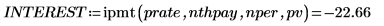
The principal payment plus the interest payment add up to the total payment PMT.

Cumulative Interest, Cumulative Principal, and APR

1. Use the cumint function to calculate the cumulative interest that is paid on the above loan:

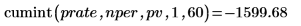
2. Use the cumprn function to calculate the cumulative principal paid on the above loan:

<region id="ID0ET2DX" top="1132.8000000000002" left="38.400000000000006" height="25.6" width="292.18333333333339" xmlns="http://schemas.mathsoft.com/worksheet50">
  <math resultRef="74">
    <eval xmlns="http://schemas.mathsoft.com/math50">
      <apply>
        <id labels="FUNCTION" xml:space="preserve">cumprn</id>
        <sequence>
          <id labels="VARIABLE" xml:space="preserve" label-is-contextual="true">prate</id>
          <id labels="VARIABLE" xml:space="preserve" label-is-contextual="true">nper</id>
          <id labels="VARIABLE" xml:space="preserve" label-is-contextual="true">pv</id>
          <real>1</real>
          <real>60</real>
        </sequence>
      </apply>
      <unitOverride>
        <placeholder />
      </unitOverride>
    </eval>
    <resultFormat>
      <decimal precision="3" show-trailing-zeros="false" radix="dec" imaginary-value="i" />
      <matrix size="12,12" offset="0,0" show-indices="false" expand-nested-arrays="false" />
    </resultFormat>
  </math>
</region>

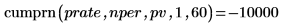
3. Use the eff function to calculate the effective Annual Percentage Rate (APR) paid on the above loan:

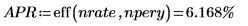
Interest Rate

1. Use the crate function to calculate the fixed interest rate per period for an investment to yield a future value fv, given a present value pv and nper number of compounding periods.

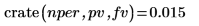
The returned value is the per period, or monthly, interest rate. This corresponds to an annual interest rate of 18%.

2. Use the nom function to calculate the nominal interest rate that corresponds to the above (APR):

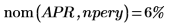
3. Use the rate function to calculate the interest rate per period of a loan over nper number of compounding periods, given a periodic, constant payment pmt and pv present value.

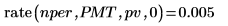
The returned value is the per period, or monthly, interest rate. This corresponds to an annual interest rate of 6%.

Number of Periods

1. Use function cnper to calculate the number of compounding periods for an investment pv to reach fv assuming you earn an annual interest rate of prate:

<region id="ID0EDIEX" top="1747.2000000000003" left="38.400000000000006" height="25.6" width="193.62666666666667" xmlns="http://schemas.mathsoft.com/worksheet50">
  <math resultRef="84">
    <eval xmlns="http://schemas.mathsoft.com/math50">
      <apply>
        <id labels="FUNCTION" xml:space="preserve">cnper</id>
        <sequence>
          <id labels="VARIABLE" xml:space="preserve" label-is-contextual="true">prate</id>
          <id labels="VARIABLE" xml:space="preserve" label-is-contextual="true">pv</id>
          <id labels="VARIABLE" xml:space="preserve" label-is-contextual="true">fv</id>
        </sequence>
      </apply>
      <unitOverride>
        <placeholder />
      </unitOverride>
    </eval>
    <resultFormat>
      <general precision="0" show-trailing-zeros="false" radix="dec" zero-threshold="15" imaginary-value="i" exponential-threshold="3" />
      <matrix size="12,12" offset="0,0" show-indices="false" expand-nested-arrays="false" />
    </resultFormat>
  </math>
</region>

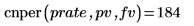
2. Use function nper to calculate the number of periods for an investment pv to reach fv assuming you make a monthly payment of PMT and earn an annual interest rate of prate:

<region id="ID0EVKEX" top="1843.2000000000003" left="38.400000000000006" height="25.6" width="250.66333333333333" xmlns="http://schemas.mathsoft.com/worksheet50">
  <math resultRef="86">
    <eval xmlns="http://schemas.mathsoft.com/math50">
      <apply>
        <id labels="FUNCTION" xml:space="preserve">nper</id>
        <sequence>
          <id labels="VARIABLE" xml:space="preserve" label-is-contextual="true">prate</id>
          <id labels="VARIABLE" xml:space="preserve" label-is-contextual="true">PMT</id>
          <id labels="VARIABLE" xml:space="preserve" label-is-contextual="true">pv</id>
          <id labels="VARIABLE" xml:space="preserve" label-is-contextual="true">fv</id>
        </sequence>
      </apply>
      <unitOverride>
        <placeholder />
      </unitOverride>
    </eval>
    <resultFormat>
      <general precision="2" show-trailing-zeros="false" radix="dec" zero-threshold="15" imaginary-value="i" exponential-threshold="3" />
    </resultFormat>
  </math>
</region>

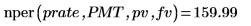
Future Value

1. Use the fv function to calculate the future value of an investment based on periodic, constant payments of PMT over nper number of compounding periods and using a fixed interest rate prate.

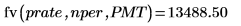
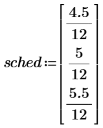
2. Use the fvadj function to calculate the future value of initial principal princ after applying a series of compound interest rates sched.

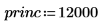
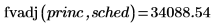
3. Use the fvc function to calculate the future value of a series of cash flows occurring at regular intervals earning an interest rate prate.