Example: Explaining Overlap When Converting Vector to Matrix
1. Define a 10000 element vector with unique data in the first 96 elements.

Element 96 is used to track the shift for different overlap values:
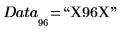
2. Define a 10 element vector of powers of 2.
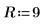 | 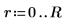 |
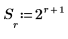 | 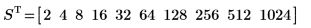 |
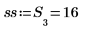 | 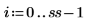 |
Where ss is the number of rows in the target matrix.
3. Define a 10 element vector of overlap factors between 0-90%, in increments of 10.
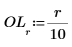 | 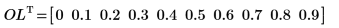 |
The overlap can not be 100%.
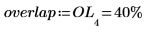
If overlap is set to zero then the Data vector is divided into a number of ss-long chunks. As the overlap increases, the number of ss-long chunks also increases, as shown by the following equation:
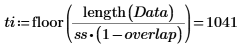
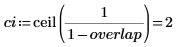
Each combination of slice size and overlap factor results in different matrix dimensions. The current settings result in these matrix dimensions:
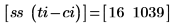
5. Create a 10 element vector TI to facilitate the setting of ti to one of ten values that are equal to or less than the value of ti.
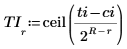 | 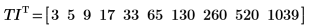 |
6. Set ti to the one of the elements of TI and create the matrix.
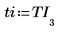 | 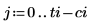 |
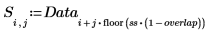 |
The new matrix dimensions are now:
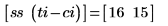
7. Use the below short program to display the content of the first 10 transposed columns of the matrix in order to observe the effect of overlap on the placement of Data element 96 "X96X".
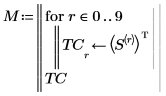
8. Evaluate matrix M.
The size of the current overlap in number of elements is a function of ss and overlap and currently equals to:
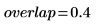 | 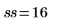 | 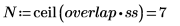 |

9. The default overlap is set to 40%. Set overlap=0 and inspect matrix M to see the data in each set.
10. Experiment with different values of overlap and use the explanations below to help you understand why "X96X" is written where it appears.
Overlap of 0%, N=0
• Set # 0 of ss elements of Data is written to column 0 of the matrix, starting at index 0.
• Set # 1 of ss elements of Data is written to column 1 of the matrix, starting at index N=0.
• Each subsequent set of ss elements is written to the subsequent column of the matrix at index N=0.
• Since the element overlap N=0, the first element of Set # 6 of ss elements, "X96X", is written to element N=0 of column 6.
Overlap of 10%, N=2
• Set # 0 of ss elements of Data is written to column 0 of the matrix, starting at index 0.
• Set # 1 of ss elements of Data is written to column 1 of the matrix, starting at index N=2. The first N elements of column 1 are filled with the last N elements of the previous column.
• Set # 2 of ss elements of Data is written to column 2 of the matrix, starting at index 2N=4. The first 2N elements of column 2 are filled with the last 2N elements of the previous column.
• Set # 3 of ss elements of Data is written to column 3 of the matrix, starting at index 3N=6. The first 3N elements of column 3 are filled with the last 3N elements of the previous column.
• Since the element overlap N=2, the first element of Set # 6 of ss elements, "X96X", is written to element 6N=12 (less than ss) of column 6.
Overlap of 20%, N=4
• The above description applies.
• When overlap=20%, N=4 and the total shift within column 6 is 6N=24 (greater than ss). This means that the shift goes beyond column 6 and into element 8 of column 7. But since the writing went into a new column, it is shifted by another N=4 and the first element of Set # 6 of ss elements, "X96X", is written to element 12 of column 7.
Overlap of 30-90%, N=5, 7, 8, 10, 12, 13, 15
• The above description applies, but overlaps between 30-90% require a closer look.
• When overlap=30%, N=5 and the total shift within column 6 is 6N=30 (greater than ss). This means that the shift goes beyond column 6 and into element 14 of column 7. But since the writing went into a new column, it is shifted by another N=5 which puts it beyond column 7 and into element 3 of column 8. But since the writing went into a new column, it is shifted by another N=5 and the first element of Set # 6 of ss elements, "X96X", is written to element 8 of column 8.
Example: Overlap of 40%, N=7
• Total shift within column 6 is 6N=42 (greater than 2ss).
• This ends up in element 10 of column 8.
• Since we shifted over 3 columns, we add 3N=21 to the shift.
• This means that "X96X", is written to element 15 of column 9.