Example: Effects of TOL and Method on Definite Integration
The Tolerance parameter
Look at how the system variable Convergence Tolerance (TOL) affects the results of definite integrals. You can set TOL on the Calculation tab, in the Worksheet Settings group, or directly in the worksheet.
1. Calculate the following integral.
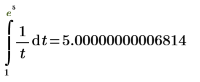
The answer is calculated using the default TOL value:
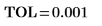
2. Loosen the tolerance and recalculate the integral.
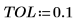
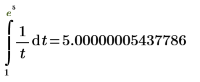
3. Tighten the tolerance and recalculate the integral.
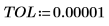
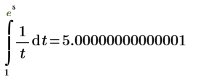
Discontinuous Functions
Discontinuous functions can become unstable at some values of integrals if they have large amplitudes and sharp discontinuities. You should determine the interval of integration that contains the bulk of the area before integrating. You can also experiment with TOL.
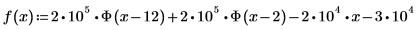
2. Define the convergence tolerance variable.
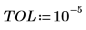
The minimum value of TOL (10-15) is too small for highly discontinuous functions, and the algorithm may return bad estimates.
3. Plot the sawtooth function f(x) and its integral function Int(x). Scale the integral function by a factor of 4.
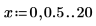
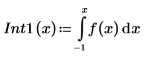
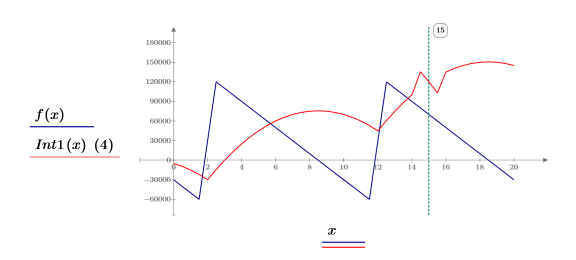
The integral function has a spike around x = 15. This can occur when integrating discontinuous functions. Decreasing TOL below 10-10 makes this even worse.
4. To get a valid answer, break the integral into pieces corresponding to the function discontinuities.
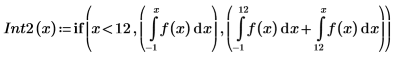
5. Plot f(x) and the newly defined Int2(x).
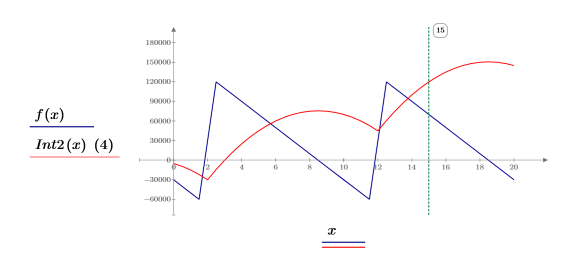
The spike around x = 15 has disappeared.
Integration Limitations
One of the limitations of numerical integration is that very narrow pulses in a mostly zero-valued function often integrate to zero. Typically, if the integrand is zero in more than 95% of the region of integration, then the algorithm may not evaluate the integrand at one of the non-zero points.
1. Define and plot a narrow pulse of width 0.05 within a zero-valued signal of width 1.0.
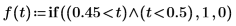
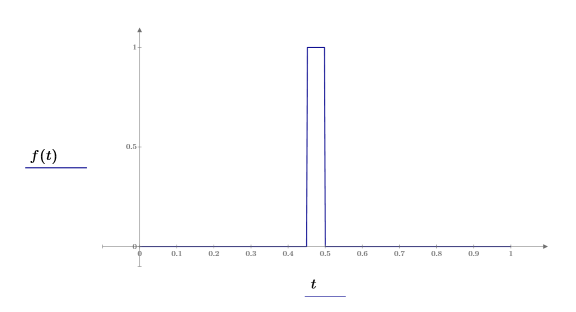
2. Calculate the numerical integral of the function.
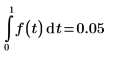
The result should equal the area of the pulse, 0.05x1.0, or 0.05.
3. Correct this problem by integrating over a smaller region containing the non-zero part of the integrand.
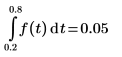
The integral returns the correct value.