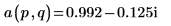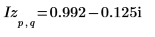Example: dft and idft of a Matrix
Use the dft and idft functions for finding the forward or inverse Discrete Fourier Transform of a matrix.
1. Define the dimensions of a data matrix.
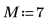
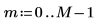
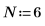
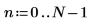
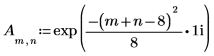
3. Use the dft function to calculate the Discrete Fourier Transform of A.
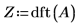
4. Use the definition of dft to calculate a specific element of Z.
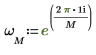
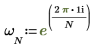
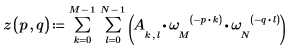
5. Use the above definition to find a specific frequency element and compare it with the output of the dft function.
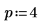
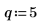
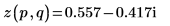
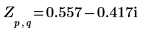
Gaussian idft
The idft function is the inverse transformation of dft. It accepts a real or complex matrix as its argument and returns a matrix of the same dimensions.
1. Show that the inverse transformation of a dft function is the function itself.
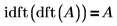
2. Use the previously defined matrix A, then show that the inverse transformation of a dft function is the function itself.
 |  |
3. Use the definition of idft to calculate any element of A.
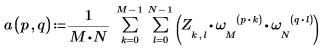
4. Use the above definition to find a specific frequency element and compare it with the corresponding element in the output of the idft function.