Example: Covariance and Correlation Coefficient
Use the cvar and corr functions to measure the strength of the correlation between two variables and to test if the data follows a linear relationship.
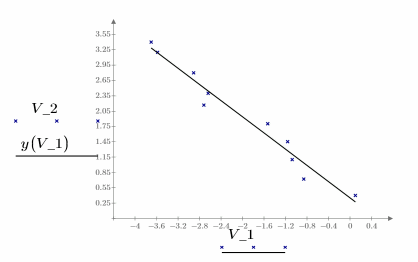
1. Examine the voltage data measured at two points of an electrical circuit.

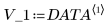
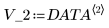
2. Plot the data and the line of best fit.
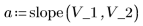
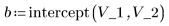
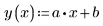
3. Calculate the covariance of the two variables.
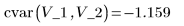
Just as variance measures how much data deviates from its mean, the covariance measures how much two data sets simultaneously deviate from their respective means.
The covariance is related to the slope of the line of best fit as follows:
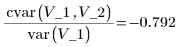
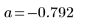
Pearson's Correlation Coefficient
1. Calculate Pearson's correlation coefficient.
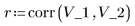
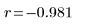
The sign of Pearson's correlation coefficient indicates the direction of the correlation. In this case, the negative sign of r indicates that V1 is inversely proportional to V2.
r lies in the interval [-1, 1]. If | r | is close to 1, this indicates that there is significant correlation. On the opposite, if | r | is close to zero, there is little evidence of correlation.
The corr function does the following calculation:
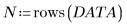
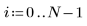
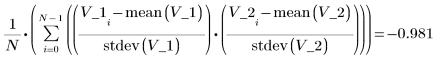
2. Calculate the coefficient of determination.
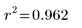
The coefficient of determination gives an equal interval and ratio measure of the strength of the correlation.
Spearman Rank Correlation
The Spearman correlation uses the same formula as Pearson's but applies it instead to the ranks of the data in each data set.
1. Rank the two sets of data.
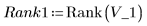 | 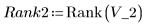 |
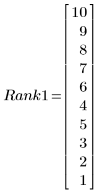 | 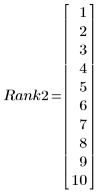 |
2. Test for correlation, comparing Spearman's rank correlation coefficient with Pearson's correlation coefficient.
◦ Spearman
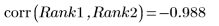
◦ Pearson
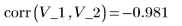
Spearman's rank coefficient is used in nonparametric hypothesis testing, that is, correlation testing that does not depend on the distribution or form of the data. It is based on the Pearson formula and has the same properties (-1 to +1). Unlike Pearson, the Spearman coefficient can be +1 or -1 without the data lying on a straight line.