Example: Cubic Spline Interpolation
Use the lspline, pspline and cspline functions to construct cubic splines (piecewise polynomials) and interpolate between data points.
1. Define a matrix.
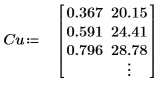
The x values fed to the spline functions must be in ascending order. |
3. Create vectors containing the x and y data.
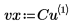
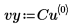
4. Use the cspline function to create a cubic spline vector, and then use the interp function to get the interpolated values.
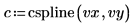
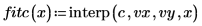
5. Use the lspline function to create a linear spline vector, and then use the interp function to get the interpolated values.
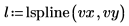
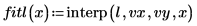
6. Use the pspline function to create a parabolic spline vector, and then use the interp function to get the interpolated values.
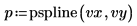
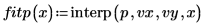
7. Plot the original data points and the cubic splines.
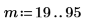
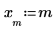
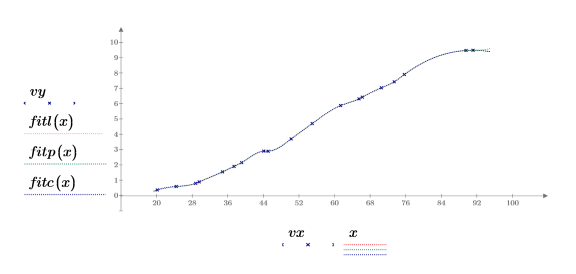
8. Zoom in on the first two data points.
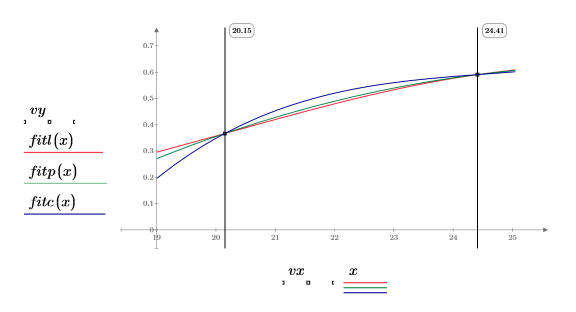
The three spline functions produce equivalent results except at the endpoints.
9. Calculate the second derivative of the interpolated linear spline vector and show that it equals 0 at the endpoints.
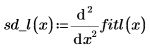 | |
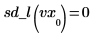 | 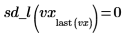 |
10. Calculate the second derivative of the interpolated parabolic spline and show that at the endpoints it equals to the value of the next nearest point.
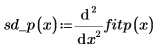
◦ Evaluate the second derivative at the first and second points and show that they are equal.
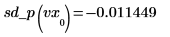
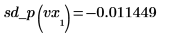
◦ Evaluate the second derivative at the second-to-last and last points and show that they are equal.
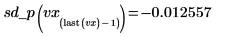
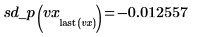
You can use the derivatives of the spline fits to find the maxima and minima, the slope, and other features of the interpolated curves.