Example: Correlation and Contingency Tables
Use Spearman's or Kendall Tau rank correlation functions to test for correlation. You can also work with contingency tables.
Functions: Spear and kendltau
A group of patients at a clinic were given different levels of a medication designed to reduce blood cholesterol. Apply the Spear and kendltau functions on the data to test for correlation between the amount of medication administered and the observed change in cholesterol.
1. Record, in units administered, the cholesterol response of 13 patients to different levels of medication. The value +1 indicates lowered cholesterol, 0 indicates no change, and -1 indicates higher cholesterol.
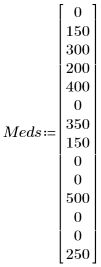 |
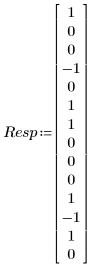 |
2. Apply the Spearman's Rank Correlation function Spear to the data.
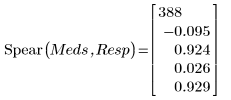
The rank-order correlation coefficient is 0.0264, nearly zero, indicating that there is very little evidence for an association between the amount of medication given and the response of the patient.
3. Apply the Kendall Tau Rank Correlation function kendltau to the data.

The correlation measure is 0.0301, again providing no support for a relationship between medication and response.
In both of these tests, the last entry in the vector gives the probability that a statistic larger in absolute value would occur for uncorrelated samples. This is based on the assumption that the test statistics are approximately normally distributed and the data are uncorrelated.
Functions: kendltau2 and contingtbl
When there are only a few possible values for each variable, you can record the data as a contingency table, with the frequency of responses as entries.
1. Construct contingency table with the frequency responses for each medication level (from left to right, the columns represent 0, 150, 250 or 500 units administered to the patients) and for each type of change observed in the patient (from top to bottom, the rows represent a decrease, no change or an increase in cholesterol).
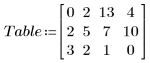
2. Apply the second Kendall Tau Rank Correlation function kendltau2 to the contingency table.
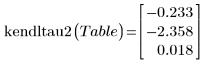
The measure of correlation is -0.2327, with probability 0.0183 that this value or one larger than this in absolute value could occur for uncorrelated samples. An interpretation of these results is that an increase in the medication is related to a decrease in cholesterol.
3. Apply the contingency function contingtbl to the contingency table.
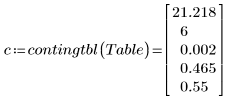
The first and second elements of c are χ2 and the degrees of freedom.
The third element of c is the probability that a computed value equal or greater than χ2 would occur if the two variables were independent. This probability is very small, which indicates that there is significant association between the level of medication and the change in cholesterol.
The strength of the association between the level of medication and the change in cholesterol is given by the last two elements of the vector: Cramer's V and the contingency coefficient. These reparametrizations of χ2 lie between 0 and 1. Unfortunately, it is difficult to interpret what these measurements mean quantitatively. They provide only qualitative guidance, in that a value near zero indicates no association, and a value near 1 indicates perfect association.