Example: Bessel Functions
Use the spherical Bessel and spherical Hankel functions to find the solutions to Schrödinger’s equation in the 3D square well (an atom).
The solution represents the allowed energies at which the inner and outer wave functions have equal values and first derivatives. These energies exist for each value of the angular momentum (L).
1. Define the mass, Plank’s constant, and radius of the nucleus:
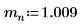
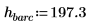
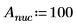
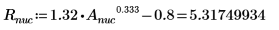
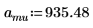
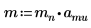
2. Set angular momentum to zero:
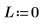
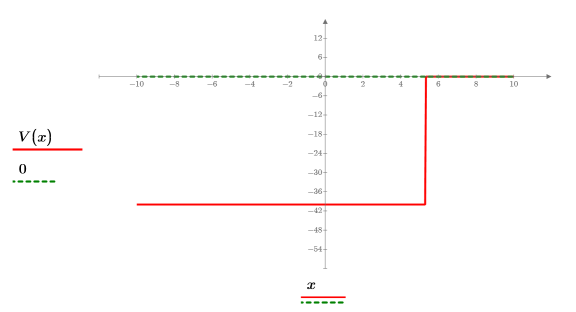
3. Define and plot the potential energy of the well:
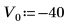
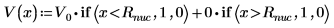
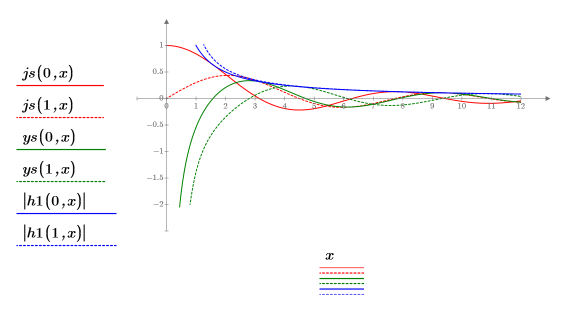
4. Use the Spherical Bessel functions and Spherical Hankel functions to find the solutions:
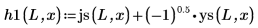
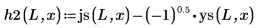
5. Define, for the bound states E < 0, the wave functions for the first energy state solution inside and outside the well:
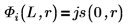
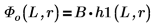
B is the relative normalization.
6. Define the propagation constants:
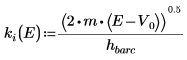
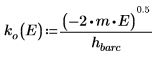
The argument for the solution outside the well is imaginary, because the wave decays outside of the potential well.
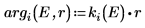
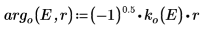
7. Match the wave functions at the edge of the well (the radius of the nucleus) to determine the relative normalization:
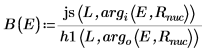
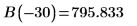
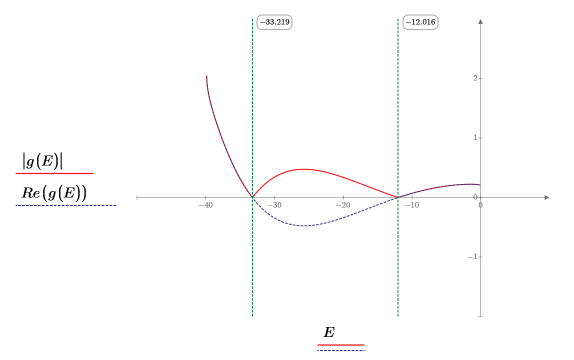
8. Match the derivatives. Determine eigenvalues by finding where the derivatives are equal.
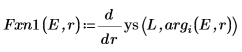
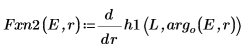
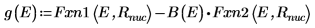
9. Provide two guess values for E:
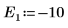
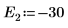
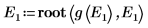
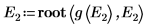
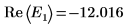
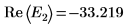
10. Plot g(E) versus E and add vertical markers to show the two root points: